gapmetric
Gap metric and Vinnicombe (nu-gap) metric for distance between two systems
Description
[
computes the gap and Vinnicombe (ν-gap) metrics for the distance between
dynamic systems gap,nugap] = gapmetric(P1,P2)P1 and P2. The gap metric values
satisfy 0 ≤ nugap ≤ gap ≤ 1. Values close to zero imply that any controller that stabilizes
P1 also stabilizes P2 with similar closed-loop
gains.
Examples
Compute Gap Metrics for Stable and Unstable Plant Models
Create two plant models. One plant, P1, is an unstable first-order system with transfer function 1/(s–0.001). The other plant, P2, is stable, with transfer function 1/(s +0.001).
P1 = tf(1,[1 -0.001]); P2 = tf(1,[1 0.001]);
Despite the fact that one plant is unstable and the other is stable, these plants are close as measured by the gap and nugap metrics.
[gap,nugap] = gapmetric(P1,P2)
gap = 0.0021
nugap = 0.0020
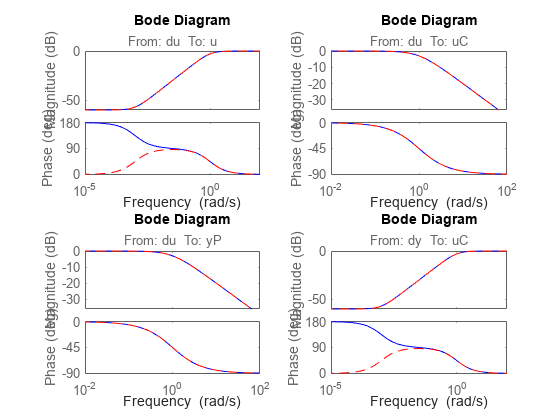
The gap is very small compared to 1. Thus a controller that yields a stable closed-loop system with P2 also tends to stabilize P1. For instance, the feedback controller C = 1 stabilizes both plants and renders nearly identical closed-loop gains. To see this, examine the sensitivity functions of the two closed-loop systems.
C = 1; H1 = loopsens(P1,C); H2 = loopsens(P2,C); subplot(2,2,1); bode(H1.Si,'-',H2.Si,'r--'); subplot(2,2,2); bode(H1.Ti,'-',H2.Ti,'r--'); subplot(2,2,3); bode(H1.PSi,'-',H2.PSi,'r--'); subplot(2,2,4); bode(H1.CSo,'-',H2.CSo,'r--');
Next, consider two stable plant models that differ by a first-order system. One plant, P3, is the transfer function 50/(s+50), and the other plant, P4, is the transfer function [50/(s+50)]*8/(s+8).
P3 = tf(50,[1 50]); P4 = tf(8,[1 8])*P3; figure bode(P3,P4)

Although the two systems have similar high-frequency dynamics and the same unity gain at low frequency, by the gap and nugap metrics, the plants are fairly far apart.
[gap,nugap] = gapmetric(P3,P4)
gap = 0.6148
nugap = 0.6147
Compute Gap Metric and Stability Margin
Consider a plant and a stabilizing controller.
P1 = tf([1 2],[1 5 10]); C = tf(4.4,[1 0]);
Compute the stability margin for this plant and controller.
b1 = ncfmargin(P1,C)
b1 = 0.1961
Next, compute the gap between P1 and the perturbed plant, P2.
P2 = tf([1 1],[1 3 10]); [gap,nugap] = gapmetric(P1,P2)
gap = 0.1391
nugap = 0.1390
Because the stability margin b1 = b(P1,C) is greater than the gap between the two plants, C also stabilizes P2. As discussed in Gap Metrics and Stability Margins, the stability margin b2 = b(P2,C) satisfies the inequality asin(b(P2,C)) ≥ asin(b1)-asin(gap). Confirm this result.
b2 = ncfmargin(P2,C); [asin(b2) asin(b1)-asin(gap)]
ans = 1×2
0.0997 0.0579
Input Arguments
P1,P2 — Input systems
dynamic system models
Input systems, specified as dynamic system models. P1 and
P2 must have the same input and output dimensions. If
P1 or P2 is a generalized state-space model
(genss or uss) then
gapmetric uses the current or nominal value of all control design
blocks.
Output Arguments
gap — Gap between P1 and P2
scalar in [0,1]
Gap between
P1 and P2, returned as a scalar in the range
[0,1]. A value close to zero implies that any controller that stabilizes
P1 also stabilizes P2 with similar closed-loop
gains. A value close to 1 means that P1 and P2 are
far apart. A value of 0 means that the two systems are identical.
nugap — Vinnicombe gap (ν-gap) between P1 and P2
scalar in [0,1]
Vinnicombe gap
(ν-gap) between P1 and P2,
returned as a scalar value in the range [0,1]. As with gap, a value
close to zero implies that any controller that stabilizes P1 also
stabilizes P2 with similar closed-loop gains. A value close to 1
means that P1 and P2 are far apart. A value of 0
means that the two systems are identical. Because 0 ≤ nugap ≤ gap ≤ 1, the ν-gap can provide a more stringent test for
robustness as described in Gap Metrics and Stability Margins.
More About
Gap Metric
Vinnicombe Gap Metric
For P1 and P2, the Vinnicombe gap metric is given by
provided that has the right winding number. Here, * denotes the conjugate (see ctranspose).
This expression is a weighted difference between the two frequency responses
P1(jω) and
P2(jω). For more information,
see Chapter 17 of [2].
Gap Metrics and Stability Margins
The gap and ν-gap metrics give a numerical value δ(P1,P2) for the distance between two LTI systems. For both metrics, the following robust performance result holds:
arcsin b(P2,C2) ≥ arcsin b(P1,C1) – arcsin δ(P1,P2) – arcsin δ(C1,C2),
where the stability margin b (see ncfmargin), assuming negative-feedback architecture, is given by
To interpret this result, suppose that a nominal plant P1 is stabilized by controller C1 with stability margin b(P1,C1). Then, if P1 is perturbed to P2 and C1 is perturbed to C2, the stability margin is degraded by no more than the above formula. For an example, see Compute Gap Metric and Stability Margin.
The ν-gap is always less than or equal to the gap, so its predictions using the above robustness result are tighter.
The quantity b(P,C)–1 is the signal gain from disturbances on the plant input and output to the input and output of the controller.
Gap Metrics in Robust Design
To make use of the gap metrics in robust design, you must introduce
weighting functions. In the robust performance formula, replace P by
W2PW1,
and replace C by . You can make similar substitutions for
P1,
P2, C1
and C2. This form makes the weighting functions
compatible with the weighting structure in the H∞
loop shaping control design procedure used by functions such as loopsyn and ncfsyn.
References
[1] Georgiou, Tryphon T. “On the Computation of the Gap Metric.” Systems & Control Letters 11, no. 4 (October 1988): 253–57. https://doi.org/10.1016/0167-6911(88)90067-9.
[2] Zhou, K., Doyle, J.C., Essentials of Robust Control. London, UK: Pearson, 1997.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)