Compare Model Discrimination and Model Calibration to Validate of Probability of Default
This example shows some differences between discrimination and calibration metrics for the validation of probability of default (PD) models.
The lifetime PD models in Risk Management Toolbox™ (see fitLifetimePDModel) support the area under the receiver operating characteristic curve (AUROC) as a discrimination (rank-ordering performance) metric and the root mean squared error (RMSE) as a calibration (predictive ability) metric. The AUROC metric measures ranking, whereas the RMSE measures the precision of the predicted values. The example shows that it is possible to have:
Same discrimination, different calibration
Same calibration, different discrimination
Therefore, it is important to look at both discrimination and calibration as part of a model validation framework.
There are several different metrics for PD model discrimination and model calibration. For more information, see References. Different metrics may have different characteristics and the behavior demonstrated in this example does not necessarily generalize to other discrimination and calibration metrics. The goal of this example is to emphasize the importance of using both discrimination and calibration metrics to assess model predictions.
Load and Fit Data
Load credit data and fit a Logistic lifetime PD model using fitLifetimePDModel.
load RetailCreditPanelData.mat data = join(data,dataMacro); pdModel = fitLifetimePDModel(data,"logistic",... 'AgeVar','YOB',... 'IDVar','ID',... 'LoanVars','ScoreGroup',... 'MacroVars',{'GDP','Market'},... 'ResponseVar','Default'); disp(pdModel)
Logistic with properties:
ModelID: "Logistic"
Description: ""
UnderlyingModel: [1x1 classreg.regr.CompactGeneralizedLinearModel]
IDVar: "ID"
AgeVar: "YOB"
LoanVars: "ScoreGroup"
MacroVars: ["GDP" "Market"]
ResponseVar: "Default"
WeightsVar: ""
TimeInterval: 1
disp(pdModel.UnderlyingModel)
Compact generalized linear regression model:
logit(Default) ~ 1 + ScoreGroup + YOB + GDP + Market
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
__________ _________ _______ ___________
(Intercept) -2.6799 0.078374 -34.193 3.0262e-256
ScoreGroup_Medium Risk -0.69409 0.028701 -24.184 3.2931e-129
ScoreGroup_Low Risk -1.2979 0.035548 -36.511 7.4134e-292
YOB -0.31534 0.010529 -29.949 4.5479e-197
GDP -0.128 0.03068 -4.1723 3.0157e-05
Market -0.0073407 0.0021916 -3.3496 0.00080942
646724 observations, 646718 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 3.2e+03, p-value = 0
Same Discrimination, Different Calibration
Discrimination measures only ranking of customers, that is, whether riskier customers get assigned higher PDs than less risky customers. Therefore, if you scale the probabilities or apply another monotonic transformation that results in valid probabilities, the AUROC measure does not change.
For example, multiply the predicted PDs by a factor of 2, which preserves the ranking (where the worse customers have higher PDs). To compare the results, pass the modified PDs as reference PDs.
PD0 = predict(pdModel,data); PD1 = 2*PD0; disp([PD0(1:10) PD1(1:10)])
0.0090 0.0181
0.0052 0.0104
0.0044 0.0088
0.0038 0.0076
0.0035 0.0071
0.0036 0.0072
0.0019 0.0037
0.0011 0.0022
0.0164 0.0328
0.0094 0.0189
Verify that the discrimination measure is not affected using modelDiscriminationPlot.
modelDiscriminationPlot(pdModel,data,'DataID','in-sample','ReferencePD',PD1,'ReferenceID','Scaled')
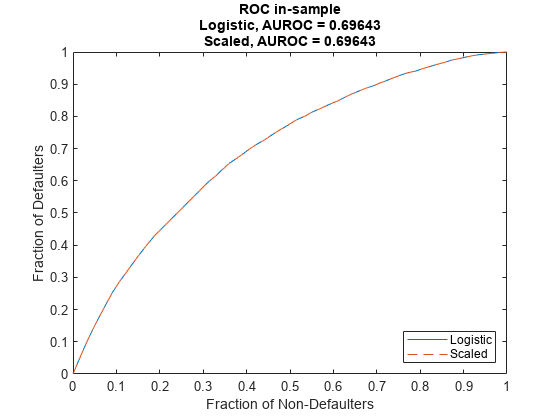
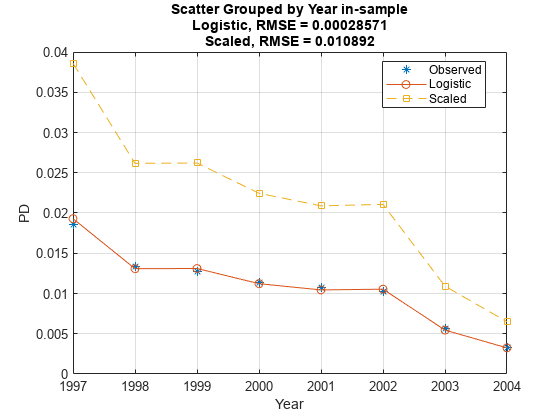
Use modelCalibrationPlot to visualize the observed default rates compared to the predicted probabilities of default (PD). The calibration, however, is severely affected by the change. The modified PDs are far away from the observed default rates and the RMSE for the modified PDs is orders of magnitude higher than the RMSE of the original PDs.
modelCalibrationPlot(pdModel,data,'Year',"DataID",'in-sample','ReferencePD',PD1,"ReferenceID",'Scaled')
Same Calibration, Different Discrimination
On the other hand, you can also modify the predicted PDs to keep the calibration metric unchanged and worsen the discrimination metric.
One way to do this is to permute the PDs within a group. By doing this, the ranking within each group is affected, but the average PD for the group is unchanged.
rng('default'); % for reproducibility PD1 = PD0; for Year=1997:2004 Ind = data.Year==Year; PDYear = PD0(Ind); PD1(Ind) = PDYear(randperm(length(PDYear))); end
Verify that the discrimination measure is worse for the modified PDs using modelDiscriminationPlot.
modelDiscriminationPlot(pdModel,data,'DataID','in-sample','ReferencePD',PD1,'ReferenceID','Permutation')

The modelCalibrationPlot function measures model calibration for PDs on grouped data. As long as the average PD for the group is unchanged, the reported calibration using the same grouping variable does not change.
modelCalibrationPlot(pdModel,data,'Year',"DataID",'in-sample','ReferencePD',PD1,"ReferenceID",'Permutation')

This example shows that discrimination and calibration metrics do not necessarily go hand in hand. Different predictions may have similar RMSE but much different AUROC, or similar AUROC but much different RMSE. Therefore, it is important to look at both discrimination and calibration as part of a model validation framework.
References
[1] Baesens, Bart, Daniel Roesch, and Harald Scheule. Credit Risk Analytics: Measurement Techniques, Applications, and Examples in SAS. Wiley, 2016.
[2] Basel Committee on Banking Supervision, "Studies on the Validation of Internal Rating Systems", Working Paper No. 14, 2005.
See Also
Probit | Logistic | Cox | modelCalibration | modelCalibrationPlot | modelDiscriminationPlot | modelDiscrimination | predictLifetime | predict | fitLifetimePDModel
Related Examples
- Basic Lifetime PD Model Validation
- Compare Logistic Model for Lifetime PD to Champion Model
- Compare Lifetime PD Models Using Cross-Validation
- Expected Credit Loss Computation
- Compare Probability of Default Using Through-the-Cycle and Point-in-Time Models
