Imitate Nonlinear MPC Controller for Flying Robot
This example shows how to train, validate, and test a deep neural network (DNN) that imitates the behavior of a nonlinear model predictive controller for a flying robot. It then compares the behavior of the deep neural network with that of the original controller. To train the deep neural network, this example uses the data aggregation (DAgger) approach as in [1].
Nonlinear model predictive control (NLMPC) solves a constrained nonlinear optimization problem in real time based on the current state of the plant. For more information on NLMPC, see Nonlinear MPC (Model Predictive Control Toolbox).
Since NLMPC solves its optimization problem in an open-loop fashion, there is the potential to replace the controller with a trained DNN. Doing so is an appealing option, since evaluating a DNN can be more computationally efficient than solving a nonlinear optimization problem in real-time.
If the trained DNN reasonably approximates the controller behavior, you can then deploy the network for your control application. You can also use the network as a warm starting point for training the actor network of a reinforcement learning agent. For an example that does so with a DNN trained for an MPC application, see Train DDPG Agent with Pretrained Actor Network.
Design Nonlinear MPC Controller
Design a nonlinear MPC controller for a flying robot. The dynamics for the flying robot are the same as in Trajectory Optimization and Control of Flying Robot Using Nonlinear MPC (Model Predictive Control Toolbox) example. First, define the limit for the control variables, which are the robot thrust levels.
umax = 3;
Create the nonlinear MPC controller object nlobj. To reduce command-window output, disable the MPC update messages. For more information, see nlmpc (Model Predictive Control Toolbox).
mpcverbosity off;
nlobj = createMPCobjImFlyingRobot(umax);Prepare Input Data
Load the input data from DAggerInputDataFileImFlyingRobot.mat. The columns of the data set contain:
is the position of the robot along the x-axis.
is the position of the robot along the y-axis.
is the orientation of the robot.
is the velocity of the robot along the x-axis.
is the velocity of the robot along the y-axis.
is the angular velocity of the robot.
is the thrust on the left side of the flying robot
is the thrust on the right side of the flying robot
is the thrust on the left side computed by NLMPC
is the thrust on the right side computed by NLMPC
The data in DAggerInputDataFileImFlyingRobot.mat is created by computing the NLMPC control action for randomly generated states (, , , , , ), and previous control actions (, ). To generate your own training data, use the collectDataImFlyingRobot function.
Load the input data.
fileName = "DAggerInputDataFileImFlyingRobot.mat";
DAggerData = load(fileName);
data = DAggerData.data;
existingData = data;
numCol = size(data,2);Create Deep Neural Network
Create the deep neural network that will imitate the NLMPC controller after training. The network architecture uses the following types of layers.
imageInputLayeris the input layer of the neural network.fullyConnectedLayermultiplies the input by a weight matrix and then adds a bias vector.reluLayeris the activation function of the neural network.tanhLayerconstrains the value to the range to [-1,1].scalingLayerscales the value to the range to [-3,3].
Define the network as an array of layer objects.
numObs = numCol-2;
numAct = 2;
hiddenLayerSize = 256;
imitateMPCNetwork = [
featureInputLayer(numObs)
fullyConnectedLayer(hiddenLayerSize)
reluLayer
fullyConnectedLayer(hiddenLayerSize)
reluLayer
fullyConnectedLayer(hiddenLayerSize)
reluLayer
fullyConnectedLayer(hiddenLayerSize)
reluLayer
fullyConnectedLayer(hiddenLayerSize)
reluLayer
fullyConnectedLayer(hiddenLayerSize)
reluLayer
fullyConnectedLayer(numAct)
tanhLayer
scalingLayer(Scale=umax)
];Plot the network.
plot(dlnetwork(imitateMPCNetwork))

Behavior Cloning Approach
One approach to learning an expert policy using supervised learning is the behavior cloning method. This method divides the expert demonstrations (NLMPC control actions in response to observations) into state-action pairs and applies supervised learning to train the network.
Specify training options.
% Initialize validation cell array validationCellArray = {0,0}; options = trainingOptions("adam", ... Metrics="rmse", ... Shuffle="every-epoch", ... MiniBatchSize=512, ... ValidationData=validationCellArray, ... InitialLearnRate=1e-3, ... ExecutionEnvironment="cpu", ... GradientThreshold=10, ... MaxEpochs=40 ... );
You can train the behavior cloning neural network by following below steps
Collect data using the
collectDataImFlyingRobotfunction.Train the behavior cloning network using the
behaviorCloningTrainNetworkfunction.

The training of the DNN using behavior cloning reduces the gap between the DNN and NLMPC performance. However, the behavior cloning neural network fails to imitate the behavior of the NLMPC controller correctly on some randomly generated data.
Training a DNN is a computationally intensive process. For this example, to save time, load a pretrained neural network object.
load("behaviorCloningMPCImDNNObject.mat");Data Aggregation Approach
To improve the performance of the DNN, you can learn the policy using an interactive demonstrator method. DAgger is an iterative method where the DNN is run in the closed-loop environment. The expert, in this case the NLMPC controller, outputs actions based on the states visited by the DNN. In this manner, more training data is aggregated and the DNN is retrained for improved performance. For more information, see [1].
Train the deep neural network using the DAggerTrainNetwork function. It creates DAggerImFlyingRobotDNNObj.mat file that contains the following information.
DatasetPath:path where the dataset corresponding to each iteration is storedpolicyObjs:policies that were trained in each iterationfinalData:total training data collected till final iterationfinalPolicy:best policy among all the collected policies
First, create and initialize the parameters for training. Use the network trained using behavior cloning (behaviorCloningNNObj.imitateMPCNetObj) as the starting point for the DAgger training.
[dataStruct,nlmpcStruct,tuningParamsStruct,neuralNetStruct] = ... loadDAggerParameters(existingData,numCol,nlobj,umax, ... options, behaviorCloningNNObj.imitateMPCNetObj);
To save time, load a pretrained neural network by setting doTraining to false. To train the DAgger yourself, set doTraining to true.
doTraining = false; if doTraining DAgger = DAggerTrainNetwork( ... nlmpcStruct, ... dataStruct, ... neuralNetStruct, ... tuningParamsStruct); else load("DAggerImFlyingRobotDNNObj.mat"); end DNN = DAgger.finalPolicy;
As an alternative, you can train the neural network with a modified policy update rule using the DAggerModifiedTrainNetwork function. In this function, after every 20 training iterations, the DNN is set to the most optimal configuration from the previous 20 iterations. To run this example with a neural network object with the modified DAgger approach, use the DAggerModifiedImFlyingRobotDNNObj.mat file.
Compare Trained DAgger Network with NLMPC Controller
To compare the performance of the NLMPC controller and the trained DNN, run closed-loop simulations with the flying robot model.
Set initial condition for the states of the flying robot (, , , , , ) and the control variables of flying robot (, ).
x0 = [-1.8200 0.5300 -2.3500 1.1700 -1.0400 0.3100]'; u0 = [-2.1800 -2.6200]';
Define simulation duration, sample time and number of simulation steps.
% Duration Tf = 15; % Sample time Ts = nlobj.Ts; % Simulation steps Tsteps = Tf/Ts+1;
Run a closed-loop simulation of the NLMPC controller.
tic [xHistoryMPC,uHistoryMPC] = ... simModelMPCImFlyingRobot(x0,u0,nlobj,Tf); toc
Elapsed time is 19.153981 seconds.
Run a closed-loop simulation of the trained DAgger network.
tic
[xHistoryDNN,uHistoryDNN] = ...
simModelDAggerImFlyingRobot(x0,u0,DNN,Ts,Tf);
tocElapsed time is 3.701377 seconds.
Plot the results, and compare the NLMPC and trained DNN trajectories.
plotSimResultsImFlyingRobot(nlobj, ...
xHistoryMPC,uHistoryMPC,xHistoryDNN,uHistoryDNN,umax,Tf);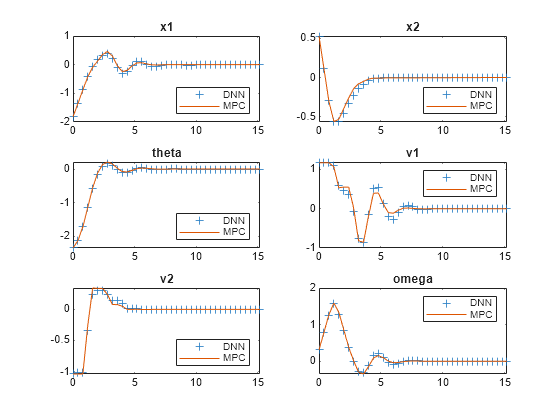

The DAgger neural network successfully imitates the behavior of the NLMPC controller. The flying robot states and control action trajectories for the controller and the DAgger deep neural network closely align. The closed-loop simulation time for the DNN is significantly less than that of the NLMPC controller.
Animate the Flying Robot with Trained DAgger Network
To validate the performance of the trained DNN, animate the flying robot with data from the DNN closed-loop simulation. The flying robot lands at the origin successfully.
Lx = 5; Ly = 5; for ct = 1:Tsteps x = xHistoryDNN(ct,1); y = xHistoryDNN(ct,2); theta = xHistoryDNN(ct,3); tL = uHistoryDNN(ct,1); tR = uHistoryDNN(ct,2); rl.env.viz.plotFlyingRobot(x,y,theta,tL,tR,Lx,Ly); pause(0.05); end

% Turn on MPC messages mpcverbosity on;
References
[1] Osa, Takayuki, Joni Pajarinen, Gerhard Neumann, J. Andrew Bagnell, Pieter Abbeel, and Jan Peters. ‘An Algorithmic Perspective on Imitation Learning’. Foundations and Trends in Robotics 7, no. 1–2 (2018): 1–179. https://doi.org/10.1561/2300000053.
See Also
Functions
trainNetwork|predict|nlmpcmove(Model Predictive Control Toolbox)
Objects
SeriesNetwork|nlmpc(Model Predictive Control Toolbox)
Topics
- Imitate MPC Controller for Lane Keeping Assist
- Train DQN Agent for Lane Keeping Assist
- Train DDPG Agent with Pretrained Actor Network
- Trajectory Optimization and Control of Flying Robot Using Nonlinear MPC (Model Predictive Control Toolbox)
- Nonlinear MPC (Model Predictive Control Toolbox)