Airborne SAR System Design
This example shows how to design a synthetic aperture radar (SAR) sensor operating in the X-band and calculate the sensor parameters. SAR uses the motion of the radar antenna over a target region to provide an image of the target region. A synthetic aperture is created when the SAR platform travels over the target region while pulses are transmitted and received from the radar antenna.
This example focuses on designing an SAR sensor to meet a set of performance parameters. It outlines the steps to translate performance specifications, such as the azimuth resolution and the probability of detection, into SAR system parameters, such as the antenna dimension and the transmit power. It models design parameters for stripmap and spotlight modes of operation. Compared to the stripmap operation, spotlight mode can provide a better resolution, and a stronger signal from the scene at the cost of reduced scene size or area imaging rate. The example also models the parameters of the azimuth chirp signal.
The diagram below classifies the various system and performance parameters. This example covers the functions for selecting system parameters to meet performance parameters.

Design Specifications
The goal of this airborne SAR system is to provide an image of the target region at a distance up to 10 km from the airborne platform with a range and azimuth resolution of 1 m. The platform is operating at an altitude of 5 km and moving at a velocity of 100 m/s. The desired performance indices are the probability of detection (Pd) and probability of false alarm (Pfa). The Pd value must be 0.9 or greater. The Pfa value must be less than 1e-6.
slantrngres = 1; % Required slant range resolution (m) azres = 1; % Required azimuth resolution (m) maxrng = 10e3; % Maximum unambiguous slant range (m) pd = 0.9; % Probability of detection pfa = 1e-6; % Probability of false alarm v = 100; % Velocity (m/s) h = 5000; % Radar altitude (m)
Airborne SAR System Design
System parameters like length of synthetic aperture, integration time, coverage rate, beamwidth for stripmap as well as spotlight modes, and signal bandwidth are key parameters that define the operational capability of a SAR system. These parameters ensure that the SAR system covers the region of interest for the calculated integration time with a wide beam. The calculated signal bandwidth meets the desired range resolution.
Signal Configuration
To calculate the SAR system parameters, you must first know the wavelength of the propagating signal, which is inversely related is to the operating frequency of the system. For this example, set the operating frequency to 10 GHz which is typical airborne SAR systems.
Use the freq2wavelen function to calculate the wavelength of the propagating signal.
freq = 10e9; % Radar frequency within X-band (Hz) lambda = freq2wavelen(freq) % Wavelength (m)
lambda = 0.0300
The signal bandwidth maps to the slant range resolution of SAR and the slant range resolution is the factor needed to distinguish two targets separated by a distance. The slant range resolution gives you the minimum range difference needed to distinguish two targets. Use the rangeres2bw function to calculate the signal bandwidth, which is determined by the slant range resolution.
pulse_bw = rangeres2bw(slantrngres) % Pulse bandwidth (Hz)pulse_bw = 149896229
Stripmap SAR Mode
Stripmap SAR mode assumes a fixed pointing direction of the radar antenna relative to the direction of motion of platform. The antenna in this example points to the broadside direction.
Antenna Orientation
The depression angle is often used to define the antenna pointing direction in elevation. This example assumes that the earth is flat so that the depression angle is the same as the grazing angle.
Use the grazingang function to calculate the grazing angle from the line-of-sight range.
grazang = grazingang(h,maxrng,'Flat') % Grazing angle (in degrees)
grazang = 30.0000
Antenna Azimuth Dimension
Next, use the sarlen and sarazres functions to analyze and calculate the synthetic aperture length and its azimuth resolution for selecting the antenna azimuth dimension. Plot the synthetic length as a function of cross-range resolution. Plot the antenna azimuth dimension as a function of synthetic length.
dazv = [1 1.5 2 2.5 3]; % Antenna azimuth dimensions (m) striplenv = zeros(1,numel(dazv)); stripazresv = zeros(1,numel(dazv)); for i=1:numel(dazv) striplenv(i) = sarlen(maxrng,lambda,dazv(i)); stripazresv(i) = sarazres(maxrng,lambda,striplenv(i)); end helperPlotStripmapMode(stripazresv,striplenv,dazv,azres)

The figures show that a synthetic aperture length of 149.9 m for stripmap mode is a good value to meet a required azimuth resolution of 1 m. The smallest antenna azimuth dimension you can use for stripmap mode in this scenario is 2 m. Decrease the antenna azimuth dimension to obtain a better azimuth resolution than 1 m for stripmap mode.
Set the synthetic aperture length to 149.9 m for stripmap mode and the antenna azimuth dimension of 2 m.
daz = 2
daz = 2
striplen = 149.9
striplen = 149.9000
Antenna Elevation Dimension
Next, determine the antenna elevation dimension based on the required swath length. For this example, assume that the required swath length is 2.4 km.
Use the aperture2swath function to analyze the swath length for selecting an antenna elevation dimension.
rngswath = 2400; delv = [0.15 0.2 0.25 0.3 0.35]; % Elevation dimensions (m) rangeswathv = zeros(1,numel(delv)); for i=1:numel(delv) [rangeswathv(i),crngswath] = aperture2swath(maxrng,lambda,[delv(i) daz],grazang); end clf plot(rangeswathv,delv) grid on xline(rngswath,'-.',{[num2str(round(rngswath,2)),' m']}); % Selected range swath xlabel('Swath Length (m)') ylabel('Antenna Elevation Dimension (m)')

The figure indicates that an antenna elevation dimension of 0.25 m is appropriate given a swath length of 2400 m.
Set the antenna elevation dimension to 0.25 m.
del = 0.25
del = 0.2500
Real Antenna Beamwidth and Gain
Use the ap2beamwidth function to calculate the real antenna beamwidth.
realAntBeamwidth = ap2beamwidth([daz del],lambda) % [Az El] (deg)realAntBeamwidth = 2×1
0.8588
6.8707
Use the aperture2gain function to calculate the antenna gain.
antGain = aperture2gain(daz*del, lambda) % dBiantGain = 38.4454
Synthetic Beamwidth, Processing Time, and Constraints
Next, use the sarbeamwidth, sarinttime, sarmaxcovrate, and sarmaxswath functions to calculate the synthetic beamwidth, integration time, area coverage rate, and maximum swath length. Notice that the azimuth beamwidth for SAR system is much smaller than the azimuth beamwidth for a real aperture radar.
stripsynbw = sarbeamwidth(lambda,striplen); % Synthetic beamwidth (degrees) stripinttime = sarinttime(v,striplen); % Integration time (s) stripcovrate = sarmaxcovrate(azres,grazang); % Upper bound on coverage rate (m^2/s) stripswlen = sarmaxswath(v,azres,grazang); % Upper bound on swath length (m) RealAntenna = [realAntBeamwidth(1); NaN; NaN; NaN]; Parameters = ["Synthetic Beamwidth";"Integration Time";"Upper Bound on Area Coverage Rate";... "Upper Bound on Swath Length"]; StripmapSAR = [stripsynbw;stripinttime;round(stripcovrate/1e6,1);round(stripswlen/1e3)]; Units = ["degrees";"s";"km^2/s";"km"]; sarparams = table(Parameters,RealAntenna,StripmapSAR,Units)
sarparams=4×4 table
Parameters RealAntenna StripmapSAR Units
___________________________________ ___________ ___________ _________
"Synthetic Beamwidth" 0.85884 0.0057294 "degrees"
"Integration Time" NaN 1.499 "s"
"Upper Bound on Area Coverage Rate" NaN 173.1 "km^2/s"
"Upper Bound on Swath Length" NaN 1731 "km"
The maximum possible azimuth resolution using SAR in this scenario is 1 m. However, to achieve this performance, pulses need to be integrated for over 1.5 s. The upper bound on the area coverage rate is 173 /s. The upper bound on the maximum swath length is 1731 km.
Spotlight SAR Mode
Spotlight SAR is capable of extending the SAR imaging capability to high resolution imaging significantly. This is possible since the spotlight mode ensures that the radar antenna squints instantaneously around the region being imaged thereby illuminating the target region for longer duration as compared to stripmap mode.
Coherent Integration Angle
The azimuth resolution in stripmap mode is 1 m in this example. The resolution of spotlight mode is often expressed in terms of coherent integration angle of the radar boresight vector as the platform traverses the synthetic aperture length.
Use the sarintang and sarlen functions to calculate the coherent integration angle and synthetic aperture length.
ciang = sarintang(lambda,azres) % (degrees)ciang = 0.8589
len = sarlen(maxrng,'CoherentIntegrationAngle',ciang) % (m)
len = 149.8976
The best possible azimuth resolution in stripmap mode is 1 m for an antenna azimuth dimension of 2 m. Use the same antenna azimuth dimension of 2 m to obtain a better azimuth resolution of 0.5 m in spotlight mode. In spotlight mode, steer the radar beam to keep the target within for a longer time and thus form a longer synthetic aperture.
Next, use the sarlen and sarazres functions to analyze the synthetic aperture length and its azimuth resolution over varying coherent integration angles.
spotazres = 0.5; % Azimuth resolution in spotlight SAR (m) intangv = 1:0.01:2.5; % Coherent integration angles (degrees) spotlenv = zeros(1,numel(intangv)); spotazresv = zeros(1,numel(intangv)); for i=1:numel(intangv) spotlenv(i) = sarlen(maxrng,'CoherentIntegrationAngle',intangv(i)); spotazresv(i) = sarazres(maxrng,lambda,spotlenv(i)); end helperPlotSpotlightMode(spotazresv,spotlenv,intangv,spotazres)
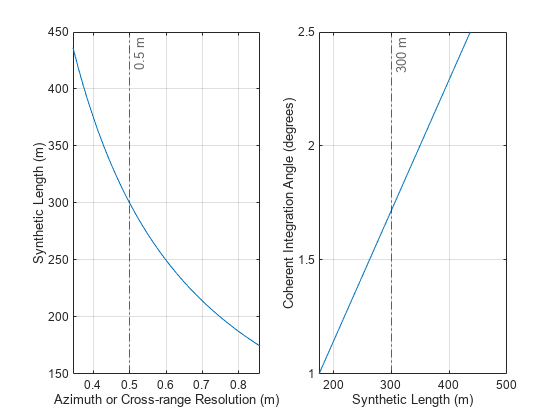
The figure indicates that in spotlight SAR mode, a synthetic aperture length of 300 m for the spotlight mode corresponding to an azimuth resolution of 0.5 m. For a coherent integration angle of 1.71 degrees, the azimuth resolution in spotlight mode is 0.5 m. It is important to note that decrease the antenna azimuth dimension to obtain a similar azimuth resolution in stripmap mode.
Set the synthetic aperture length to 300 m and the coherent integration angle to 1.71 degrees for spotlight mode.
spotlen = 300
spotlen = 300
intang = 1.71
intang = 1.7100
Synthetic Beamwidth, Processing Time, and Constraint
Compared to the stripmap mode, spotlight mode can provide a better resolution, and a stronger signal from the scene at the cost of reduced scene size or area imaging rate.
Use the sarbeamwidth, sarinttime, sarmaxcovrate, and sarmaxswath functions to calculate the synthetic beamwidth, integration time, area coverage rate, and maximum swath length. Notice that the area coverage rate and maximum swath length for spotlight SAR system are much smaller than for stripmap mode.
spotsynbw = sarbeamwidth(lambda,spotlen); % Synthetic beamwidth (degrees) spotinttime = sarinttime(v,spotlen); % Integration time (s) spotcovrate = sarmaxcovrate(spotazres,grazang); % Upper bound on coverage rate (m^2/s) spotswlen = sarmaxswath(v,spotazres,grazang); % Upper bound on swath length (m) SpotlightSAR = [spotsynbw;spotinttime;round(spotcovrate/1e6,1);round(spotswlen/1e3)]; sar = table(Parameters,StripmapSAR,SpotlightSAR,Units)
sar=4×4 table
Parameters StripmapSAR SpotlightSAR Units
___________________________________ ___________ ____________ _________
"Synthetic Beamwidth" 0.0057294 0.0028628 "degrees"
"Integration Time" 1.499 3 "s"
"Upper Bound on Area Coverage Rate" 173.1 86.5 "km^2/s"
"Upper Bound on Swath Length" 1731 865 "km"
Azimuth Chirp Signal Parameters
Determine the azimuth chirp signal parameters which are the azimuth chirp rate, Doppler bandwidth, beam compression ratio, and azimuth bandwidth after dechirp. You can derive the azimuth time-bandwidth product. These are important for designing an accurate synthetic aperture processing mechanism in azimuth.
Use the sarchirprate function to calculate the azimuth chirp rate, which is the rate at which the azimuth signal changes frequency as the sensor illuminates a scatterer.
azchirp = sarchirprate(maxrng,lambda,v); % (Hz/s)Analyze the azimuth chirp rate sensitivity to range and Doppler cone angle variations. The plot shows that increasing the unambiguous range of the radar reduces the azimuth chirp rate.
dcang = 60:1:120; % Doppler cone angles (in degrees) rngv = 1e3:100:maxrng; azchirpv = zeros(length(dcang),length(rngv)); for i = 1:length(dcang) azchirpv(i,:) = sarchirprate(rngv,lambda,v,dcang(i)); end clf mesh(rngv/1e3,dcang,azchirpv) xlabel('Range (km)') ylabel('Doppler Cone Angle (degrees)') zlabel('Azimuth Chirp Rate (Hz/s)') view([45 45]);

Use the sarscenedopbw function to calculate the scene bandwidth after azimuth dechirping. Assume a scene size of 916 m.
Wa = 916;
bwdechirp = sarscenedopbw(maxrng,lambda,v,Wa); % (Hz)Analyze the scene bandwidth sensitivity to Doppler cone angle variations.
bwdechirpv = zeros(length(dcang),1); for i = 1:length(dcang) bwdechirpv(i,:) = sarscenedopbw(maxrng,lambda,v,Wa,dcang(i)); end clf plot(dcang,bwdechirpv) grid on xlabel('Doppler Cone Angle (degrees)') ylabel('Azimuth Bandwidth after Dechirp (Hz)')

Next, use the sarpointdopbw and sarbeamcompratio functions to calculate the Doppler bandwidth of the received signal from a point scatterer and the beam compression ratio. Notice that the Doppler bandwidth, and beam compression ratio for a spotlight SAR mode are much greater than for stripmap SAR mode.
% Stripmap SAR Mode stripbwchirp = sarpointdopbw(v,azres); % (Hz) striptbwaz = bwdechirp*stripinttime; % Unitless stripbcr = sarbeamcompratio(maxrng,lambda,striplen,Wa); % Unitless % Spotlight SAR Mode spotbwchirp = sarpointdopbw(v,spotazres); % (Hz) spottbwaz = bwdechirp*spotinttime; % Unitless spotbcr = sarbeamcompratio(maxrng,lambda,spotlen,Wa); % Unitless Parameters = ["Doppler Bandwidth from Point Scatterer";"Azimuth Time-Bandwidth Product";... "Beam Compression Ratio";"Azimuth Chirp Rate";"Azimuth Bandwidth after Dechirp"]; StripmapSAR = [stripbwchirp;striptbwaz;stripbcr;round(azchirp);bwdechirp]; SpotlightSAR = [spotbwchirp;round(spottbwaz);round(spotbcr);round(azchirp);bwdechirp]; Units = ["Hz";"unitless";"unitless";"Hz/s";"Hz"]; r = table(Parameters,StripmapSAR,SpotlightSAR,Units)
r=5×4 table
Parameters StripmapSAR SpotlightSAR Units
________________________________________ ___________ ____________ __________
"Doppler Bandwidth from Point Scatterer" 100 200 "Hz"
"Azimuth Time-Bandwidth Product" 916.02 1833 "unitless"
"Beam Compression Ratio" 916.02 1833 "unitless"
"Azimuth Chirp Rate" 67 67 "Hz/s"
"Azimuth Bandwidth after Dechirp" 611.09 611.09 "Hz"
SAR Power Calculation
Estimate the peak power that must be transmitted using the power form of the radar equation for stripmap SAR mode. The required peak power depends upon many factors, including the maximum unambiguous range, the required SNR at the receiver, and the pulse width of the waveform. Among these factors, the required SNR at the receiver is determined by the design goal for the Pd and Pfa. Model and estimate the target RCS, the PRF, and different sources of gain and loss for the radar system and its environment.
Receiver SNR
First, calculate the SNR required at the receiver. The relation between Pd, Pfa, and SNR can be best represented by a receiver operating characteristics (ROC) curve.
snr_db = [-inf, 0, 3, 10, 13]; rocsnr(snr_db);

The ROC curves show that to satisfy the design goals of Pfa = 1e-6 and Pd = 0.9, the SNR of the received signal must exceed 13 dB. You can surmise the SNR value by looking at the plot, but calculating only the required value is more straightforward. Using the albersheim function, derive the required SNR.
snr_min = albersheim(pd, pfa)
snr_min = 13.1145
Target RCS
Use the landreflectivity function to calculate the reflectivity, which is the normalized radar cross-section (NRCS) for a given grazing angle and operating frequency. Then calculate the target RCS in the ground image plane using the sarSurfaceRCS function and taking the radar resolution into account.
landType = "Smooth"; nrcs = landreflectivity(landType,grazang,freq); % Calculate normalized RCS of smooth land with no vegetation tgtrcs = sarSurfaceRCS(nrcs,[slantrngres azres],grazang);
Upper and Lower PRF Bounds
Use the sarprfbounds function to determine the minimum and maximum PRF values for a range swath and azimuth resolution given the radar velocity and the grazing angle.
[prfminv, prfmax] = sarprfbounds(v,azres,rngswath,grazang)
prfminv = 100
prfmax = 6.7268e+04
PRF Selection
The PRF is typically programmable and can be optimized for each application. Use the sarprf function to calculate the PRF of the radar based on the radar velocity and the real antenna dimension along the azimuth. Specify a constant roll-off factor as a safety margin to prevent mainlobe returns from aliasing in the PRF interval. If the PRF is set too low, the radar suffers from grating lobes and Doppler ambiguities. If the PRF is set too high, range measurements will be ambiguous.
prf = sarprf(v,daz,'RollOff',1.5)prf = 150
The selected PRF is within the PRF bounds.
Processing Gains
Use the matchinggain function to calculate the range processing gain due to the noise bandwidth reduction after the matched filter.
d = 0.05; % 5 percent duty cycle pw = (1/prf)*d; % Effective pulse width (s) rnggain = matchinggain(pw,pulse_bw) % Range processing gain (dB)
rnggain = 46.9867
Use the sarazgain function to calculate the azimuth processing gain due to the coherent integration of pulses.
azgain = sarazgain(maxrng,lambda,v,azres,prf); % Az processing gain (dB)Losses and Noise Factor
Use the noisefigure function to estimate the noise figure of the cascaded receiver stages. Assume seven stages with the following values:
Stage 1 LNA: Noise Figure = 1.0 dB, Gain = 15.0
Stage 2 RF Filter: Noise Figure = 0.5 dB, Gain = -0.5
Stage 3 Mixer: Noise Figure = 5.0 dB, Gain = -7.0
Stage 4 IF Filter: Noise Figure = 1.0 dB, Gain = -1.0
Stage 5 IF Preamplifier: Noise Figure = 0.6 dB, Gain = 15.0
Stage 6 IF Stages: Noise Figure = 1.0 dB, Gain = 20.0
Stage 7 Phase Detectors: Noise Figure = 6.0 dB, Gain = -5.0
nf = [1.0, 0.5, 5.0, 1.0, 0.6, 1.0, 6.0]; % dB g = [15.0, -0.5, -7.0, -1.0, 15.0, 20.0, -5.0]; % dB cnf = noisefigure(nf, g)
cnf = 1.5252
Use the radarpropfactor function to calculate the one-way radar propagation factor over smooth land.
[hgtsd, beta0, vegType] = landroughness('Smooth'); tgtheight = hgtsd; Re = effearthradius(maxrng,h,tgtheight); propf = radarpropfactor(maxrng,freq,h,tgtheight,'EffectiveEarthradius',Re,'TiltAngle',grazang,... 'ElevationBeamwidth',realAntBeamwidth(2),'SurfaceHeightStandardDeviation',hgtsd,'SurfaceSlope',beta0,... 'VegetationType',vegType)
propf = -26.5098
Use the tropopl function to calculate losses due to atmospheric gaseous absorption.
atmoLoss = tropopl(maxrng,freq,tgtheight,grazang)
atmoLoss = 0.0731
Transmit Power
A finite data collection time limits the total energy collected, and signal processing in the radar increases the SNR in the SAR image. The image SNR is given by
where is the SNR gain due to range processing and is the gain due to azimuth processing. The product is referred to as the signal processing gain. In decibels, this becomes addition as shown in the code below.
% Calculate the image SNR imgsnr = snr_min + rnggain + azgain; % Image SNR (dB)
Use the radareqsarpow function to calculate the peak power with the SAR radar equation. You can also specify additional losses and factors, including the azimuth beam shape loss, window loss, transmission loss, and receive line loss. Estimate the beam shape loss with the beamloss function, and use 5 dB for all other fixed losses combined. Note that the radareqsarpow function assumes that the effective noise bandwidth can be approximated as , where is the pulsewidth in seconds.
% Calculate required transmitted power Lb = beamloss; % Beam loss (dB) customLoss = 5; % Custom system losses (dB) sysLosses = customLoss + Lb; % Combined losses (dB) sntemp = systemp(cnf); % Noise temperature (K) Pt = radareqsarpow(maxrng,lambda,imgsnr,pw,rnggain,azgain,'Gain',antGain,'RCS',tgtrcs,... 'AtmosphericLoss',atmoLoss,'Loss',sysLosses,'PropagationFactor',propf,... 'Ts',sntemp)
Pt = 7.5337e+07
Summary
This example shows the aspects that must be calculated to design an X-band SAR system that can operate in stripmap and spotlight mode. The example shows that the same SAR system can operate in stripmap as well as spotlight modes and achieve varying levels of resolution depending upon the requirements at the cost of other parameters. First, you analyze and select the antenna dimensions to meet the required resolutions. Then you estimate the antenna gains, processing time, constraints, and the azimuth chirp signal parameters. Then estimate the required SNR, target RCS, PRF, processing gains and losses in the radar and its environment. Finally, you use the SAR equation to calculate the peak transmit power.
Parameters = ["Antenna Dimension in Azimuth";"Antenna Dimension in Elevation";"Synthetic Aperture Length";... "Azimuth Resolution";"Synthetic Beamwidth";"Integration Time";"Upper Bound on Area Coverage Rate";... "Upper Bound on Swath Length";"Coherent Integration Angle";"Doppler Bandwidth from Point Scatterer";... "Azimuth Time-Bandwidth Product";"Beam Compression Ratio";"Azimuth Chirp Rate";"Azimuth Bandwidth after Dechirp"]; Stripmap = [daz;del;striplen;azres;stripsynbw;stripinttime;round(stripcovrate/1e6,1);round(stripswlen/1e3);... NaN;stripbwchirp;striptbwaz;stripbcr;round(azchirp);bwdechirp]; Spotlight = [daz;del;spotlen;spotazres;spotsynbw;spotinttime;round(spotcovrate/1e6,1);round(spotswlen/1e3);... intang;spotbwchirp;round(spottbwaz);round(spotbcr);round(azchirp);bwdechirp]; Units = ["m";"m";"m";"m";"degrees";"s";"km^2/s";"km";"degrees";"Hz";"unitless";... "unitless";"Hz/s";"Hz"]; T = table(Parameters,Stripmap,Spotlight,Units)
T=14×4 table
Parameters Stripmap Spotlight Units
________________________________________ _________ _________ __________
"Antenna Dimension in Azimuth" 2 2 "m"
"Antenna Dimension in Elevation" 0.25 0.25 "m"
"Synthetic Aperture Length" 149.9 300 "m"
"Azimuth Resolution" 1 0.5 "m"
"Synthetic Beamwidth" 0.0057294 0.0028628 "degrees"
"Integration Time" 1.499 3 "s"
"Upper Bound on Area Coverage Rate" 173.1 86.5 "km^2/s"
"Upper Bound on Swath Length" 1731 865 "km"
"Coherent Integration Angle" NaN 1.71 "degrees"
"Doppler Bandwidth from Point Scatterer" 100 200 "Hz"
"Azimuth Time-Bandwidth Product" 916.02 1833 "unitless"
"Beam Compression Ratio" 916.02 1833 "unitless"
"Azimuth Chirp Rate" 67 67 "Hz/s"
"Azimuth Bandwidth after Dechirp" 611.09 611.09 "Hz"
References
Carrara, Walter G., Ronald M. Majewski, and Ron S. Goodman. Spotlight Synthetic Aperture Radar: Signal Processing Algorithms. Boston: Artech House, 1995.
Doerry, Armin W. “Performance Limits for Synthetic Aperture Radar.” 2nd edition, Sandia Report, SAND2006-0821, February 2006.
Supporting Functions
helperPlotStripmapMode
function helperPlotStripmapMode(stripazresv,striplenv,dazv,azres) % Plot azimuth resolution vs. synthetic aperture length subplot(1,2,1) plot(stripazresv,striplenv) grid on xline(azres,'-.',{[num2str(round(azres)),' m']}); % Selected azimuth resolution xlabel('Azimuth or Cross-range Resolution (m)') ylabel('Synthetic Length (m)') stripidx = find(abs(striplenv-150)<1); % Index corresponding to required azimuth resolution % Plot synthetic aperture length vs. antenna azimuth dimensions subplot(1,2,2) plot(striplenv,dazv) grid on xline(striplenv(stripidx),'-.',{[num2str(round(striplenv(stripidx),2)),' m']}); % Selected synthetic length xlabel('Synthetic Length (m)') ylabel('Antenna Azimuth Dimension (m)') end
helperPlotSpotlightMode
function helperPlotSpotlightMode(spotazresv,spotlenv,intangv,spotazres) % Plot azimuth resolution vs. synthetic aperture length subplot(1,2,1) plot(spotazresv,spotlenv) grid on xline(0.5,'-.',{[num2str(round(spotazres,2)),' m']}); % Selected azimuth resolution xlabel('Azimuth or Cross-range Resolution (m)') ylabel('Synthetic Length (m)') spotidx = find(abs(spotlenv-300)<1); % Index corresponding to 0.5 m azimuth resolution % Plot synthetic aperture length vs. coherent integration angles subplot(1,2,2) plot(spotlenv,intangv) grid on xline(spotlenv(spotidx),'-.',{[num2str(round(spotlenv(spotidx))),' m']}); % Selected synthetic length xlabel('Synthetic Length (m)') ylabel('Coherent Integration Angle (degrees)') end