Discrete PI Controller with Integral Anti-Windup
Discrete-time PI control with integral anti-windup
Libraries:
Simscape /
Electrical /
Control /
General Control
Description
The Discrete PI Controller with Integral Anti-Windup block implements discrete PI control with internal anti-windup. The figure shows the equivalent circuit for the controller with internal anti-windup.
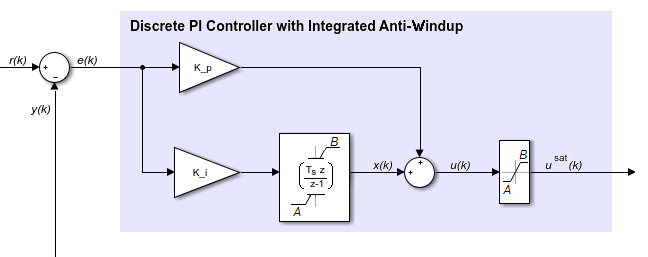
Equations
The block calculates the control signal using the backward Euler discretization method:
where:
u is the control signal.
Kp is the proportional gain coefficient.
e is the error signal.
Ki is the integral gain coefficient.
Ts is the sampling period.
A is the lower limit for saturation.
B is the upper limit for saturation.
Examples
Ports
Input
Output
Parameters
References
[1] IEEE Recommended Practice for Excitation System Models for Power System Stability Studies. IEEE Std 421.5/D39. Piscataway, NJ: IEEE-SA, 2015.
Extended Capabilities
Version History
Introduced in R2017b