Specify Nonconstant PDE Coefficients
When solving PDEs with nonconstant coefficients, specify these coefficients by using function handles. This example shows how to write functions to represent nonconstant coefficients for PDE problems.
Geometry and Mesh
Create a model.
model = createpde;
Include a unit square geometry in the model.
geometryFromEdges(model,@squareg);
Generate a mesh with a maximum edge length of 0.25. Plot the mesh.
generateMesh(model,Hmax=0.25); pdemesh(model)
Function for Nonconstant Coefficient f
Write a function that returns the value for the nonconstant coefficient f. The function
must accept two input arguments, location and
state. The solvers automatically compute and populate the data in
the location and state structure arrays and pass
this data to your function. To visualize the location data used by
the toolbox, add the scatter plot command to your function.
function fcoeff = fcoefffunc(location,state) fcoeff = location.x.^2.*sin(location.y); scatter(location.x,location.y,".","black"); hold on end

Specify the PDE coefficients using the function that you wrote for the f coefficient.
specifyCoefficients(model,m0,d=0,c=1,a=0,f=@fcoefffunc);
Apply the Dirichlet boundary condition u = 0 for all edges of the square.
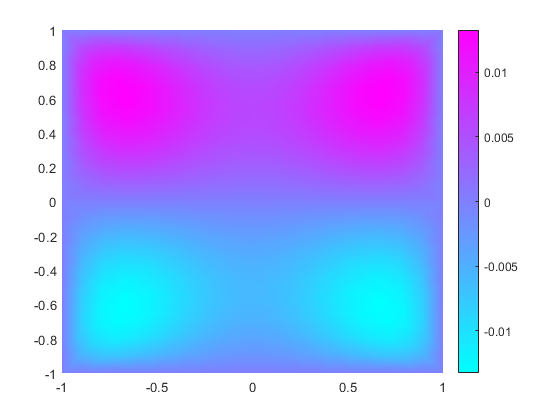
applyBoundaryCondition(model,"dirichlet",Edge=1:4,u=0);Solve the equation and plot the solution.
results = solvepde(model); figure pdeplot(model,XYData=results.NodalSolution)
Anonymous Function for a PDE Coefficient
If the dependency of a coefficient on coordinates, time, or solution is simple, you
can use an anonymous function to represent the nonconstant PDE coefficient. Thus, you
can implement the dependency shown earlier in this example as the
fcoefffunc function, as this anonymous function.
f = @(location,state)location.x.^2.*sin(location.y);
Specify the PDE coefficients.
specifyCoefficients(model,m=0,d=0,c=1,a=0,f=f);
Additional Arguments
If a function that represents a nonconstant PDE coefficient requires more arguments
than location and state, follow these
steps:
Write a function that takes the
locationandstatearguments and the additional arguments.Wrap that function with an anonymous function that takes only the
locationandstatearguments.
For example, define the coefficient f as . First, write the function that takes the arguments
a, b, and c in addition to
the location and state arguments.
function fcoeff = fcoefffunc_abc(location,state,a,b,c) fcoeff = a*location.x.^2.*sin(b*location.y) + c; end
Because functions defining nonconstant coefficients must have exactly two arguments,
wrap the fcoefffunc_abc function with an anonymous function.
fcoefffunc_add_args = ...
@(location,state) fcoefffunc_abc(location,state,1,2,3);Now you can use fcoefffunc_add_args to specify the coefficient
f.
specifyCoefficients(model,m=0,d=0,c=1,a=0,f=fcoefffunc_add_args);