Geometry from alphaShape

Create a 3-D geometry using the MATLAB® alphaShape function. First, create an alphaShape object of a block with a cylindrical hole. Then create a geometry from the alphaShape boundary.

Create a 2-D mesh grid.

[xg,yg] = meshgrid(-3:0.25:3);
xg = xg(:);
yg = yg(:);

Create a unit disk. Remove all the mesh grid points that fall inside the unit disk, and include the unit disk points.

t = (pi/24:pi/24:2*pi)';
x = cos(t);
y = sin(t);
circShp = alphaShape(x,y,2);
in = inShape(circShp,xg,yg);
xg = [xg(~in); cos(t)];
yg = [yg(~in); sin(t)];

Create 3-D copies of the remaining mesh grid points, with the z-coordinates ranging from 0 through 1. Combine the points into an alphaShape object.

zg = ones(numel(xg),1);
xg = repmat(xg,5,1);
yg = repmat(yg,5,1);
zg = zg*(0:.25:1);
zg = zg(:);
shp = alphaShape(xg,yg,zg);

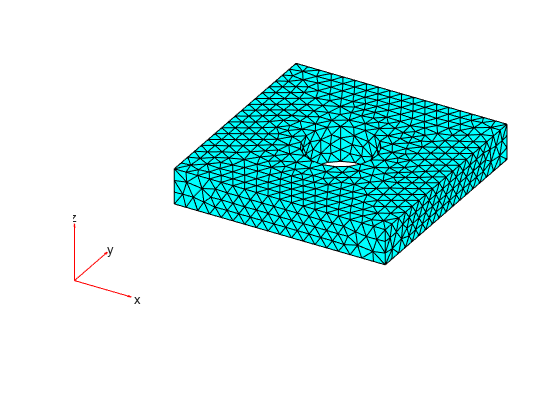
Generate a surface mesh of the alphaShape object.

[elements,nodes] = boundaryFacets(shp);

Create an fegeometry object from the surface mesh.

gm = fegeometry(nodes,elements)

gm = 
  fegeometry with properties:

       NumCells: 1
       NumFaces: 7
       NumEdges: 14
    NumVertices: 10
       Vertices: [10x3 double]
           Mesh: []

For a 3-D geometry created from the surface mesh, the Mesh property remains empty. To use the geometry in an analysis, generate a mesh.

gm = generateMesh(gm);
gm.Mesh

ans = 
  FEMesh with properties:

             Nodes: [3x11247 double]
          Elements: [10x6880 double]
    MaxElementSize: 0.3418
    MinElementSize: 0.1709
     MeshGradation: 1.5000
    GeometricOrder: 'quadratic'

Plot the geometry with the face labels.

pdegplot(gm,FaceLabels="on",FaceAlpha=0.5);

Plot the mesh.

pdemesh(gm);