Or Instead of And Constraints
In general, solvers takes constraints with an implicit AND:
constraint 1 AND constraint 2 AND constraint 3 are all satisfied.
However, sometimes you want an OR:
constraint 1 OR constraint 2 OR constraint 3 is satisfied.
These formulations are not logically equivalent, and there is generally no way to express OR constraints in terms of AND constraints.
Tip
Fortunately, nonlinear constraints are extremely flexible. You get OR constraints simply by setting the nonlinear constraint function to the minimum of the constraint functions.
The reason that you can set the minimum as the constraint is due to the nature of Nonlinear Constraints: you give them as a set of functions that must be negative at a feasible point. If your constraints are
F1(x) ≤ 0 OR F2(x) ≤ 0 OR F3(x) ≤ 0,
then set the nonlinear inequality constraint function c(x) as:
c(x) = min(F1(x),F2(x),F3(x)).
c(x) is not smooth, which is a general requirement for constraint functions, due to the minimum. Nevertheless, the method often works.
Note
You cannot use the usual bounds and linear constraints in an OR constraint. Instead, convert your bounds and linear constraints to nonlinear constraint functions, as in this example.
For example, suppose your feasible region is the L-shaped region: x is in the rectangle –1 ≤ x(1) ≤ 1, 0 ≤ x(2) ≤ 1 OR x is in the rectangle 0 ≤ x(1) ≤ 1, –1 ≤ x(2) ≤ 1.
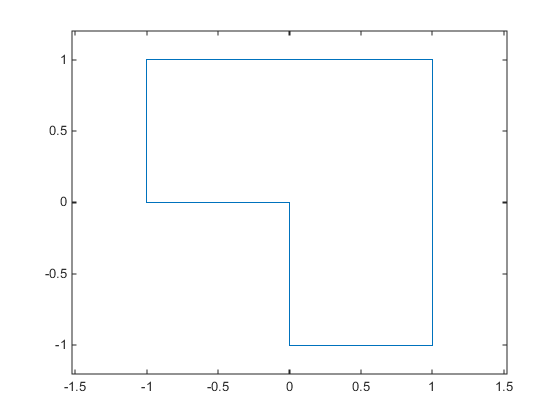
To represent a rectangle as a nonlinear constraint, instead of as bound constraints, construct a function that is negative inside the rectangle a ≤ x(1) ≤ b, c ≤ x(2) ≤ d:
function cout = rectconstr(x,a,b,c,d) % Negative when x is in the rectangle [a,b][c,d] % First check that a,b,c,d are in the correct order if (b <= a) || (d <= c) error('Give a rectangle a < b, c < d') end cout = max([(x(1)-b),(x(2)-d),(a-x(1)),(c-x(2))]);
Following the prescription of using the minimum of nonlinear constraint functions, for the L-shaped region, the nonlinear constraint function is:
function [c,ceq] = rectconstrfcn(x) ceq = []; % no equality constraint F(1) = rectconstr(x,-1,1,0,1); % one rectangle F(2) = rectconstr(x,0,1,-1,1); % another rectangle c = min(F); % for OR constraints
Suppose your objective function is
fun = @(x)exp(x(1)) * (4*x(1)^2 + 2*x(2)^2 + 4*x(1)*x(2) + 2*x(2) + 1);
Minimize fun over the L-shaped region:
opts = optimoptions(@fmincon,'Algorithm','interior-point','Display','off'); x0 = [-.5,.6]; % an arbitrary guess [xsol,fval,eflag] = fmincon(fun,x0,[],[],[],[],[],[],@rectconstrfcn,opts)
xsol =
0.4998 -0.9996
fval =
2.4650e-07
eflag =
1Clearly, the solution xsol is inside the L-shaped region. The exit
flag is 1, indicating that xsol is a local
minimum.
