Multi-Objective Goal Attainment Optimization
This example shows how to solve a pole-placement problem using the multiobjective goal attainment method. This algorithm is implemented in the function fgoalattain.
Equation that Describes Evolution of System
Consider a 2-input 2-output unstable plant. The equation describing the evolution of the system is
where is the input (control) signal. The output of the system is
The matrices , , and are
A = [ -0.5 0 0; 0 -2 10; 0 1 -2 ]; B = [ 1 0; -2 2; 0 1 ]; C = [ 1 0 0; 0 0 1 ];
Optimization Objective
Suppose that the control signal is set as proportional to the output :
for some matrix .
This means that the evolution of the system is:
The object of the optimization is to design to have the following two properties:
1. The real parts of the eigenvalues of are smaller than [–5, –3, –1]. (This is called pole placement in the control literature.)
2. abs() <= 4 (each element of is between -4 and 4)
In order to solve the optimization, first set the multiobjective goals:
goal = [-5, -3, -1];
Set the weights equal to the goals to ensure same percentage under- or over-attainment in the goals.
weight = abs(goal);
Initialize the output feedback controller
K0 = [ -1 -1; -1 -1];
Set upper and lower bounds on the controller
lb = repmat(-4,size(K0))
lb = 2×2
-4 -4
-4 -4
ub = repmat(4,size(K0))
ub = 2×2
4 4
4 4
Set optimization display parameter to give output at each iteration:
options = optimoptions('fgoalattain','Display','iter');
Create a vector-valued function eigfun that returns the eigenvalues of the closed loop system. This function requires additional parameters (namely, the matrices , , and ); the most convenient way to pass these is through an anonymous function:
eigfun = @(K) sort(eig(A+B*K*C));
Call Optimization Solver
To begin the optimization we call fgoalattain:
[K,~,attainfactor] = ...
fgoalattain(eigfun,K0,goal,weight,[],[],[],[],lb,ub,[],options); Attainment Max Line search Directional
Iter F-count factor constraint steplength derivative Procedure
0 6 0 1.88521
1 13 1.031 0.02998 1 0.745
2 20 0.3525 0.06863 1 -0.613
3 27 -0.1706 0.1071 1 -0.223 Hessian modified
4 34 -0.2236 0.06654 1 -0.234 Hessian modified twice
5 41 -0.3568 0.007894 1 -0.0812
6 48 -0.3645 0.000145 1 -0.164 Hessian modified
7 55 -0.3645 0 1 -0.00515 Hessian modified
8 62 -0.3675 0.0001548 1 -0.00812 Hessian modified twice
9 69 -0.3889 0.008327 1 -0.00751 Hessian modified
10 76 -0.3862 0 1 0.00568
11 83 -0.3863 4.469e-13 1 -0.998 Hessian modified twice
Local minimum possible. Constraints satisfied.
fgoalattain stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are
satisfied to within the value of the constraint tolerance.
<stopping criteria details>
The value of the control parameters at the solution is:
K
K = 2×2
-4.0000 -0.2564
-4.0000 -4.0000
The eigenvalues of the closed loop system are in eigfun(K) as follows: (they are also held in output fval)
eigfun(K)
ans = 3×1
-6.9313
-4.1588
-1.4099
The attainment factor indicates the level of goal achievement. A negative attainment factor indicates over-achievement, positive indicates under-achievement. The value attainfactor we obtained in this run indicates that the objectives have been over-achieved by almost 40 percent:
attainfactor
attainfactor = -0.3863
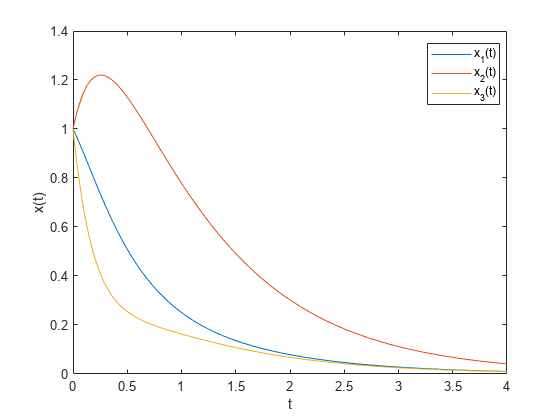
Evolution of System Via Solution to ODE
Here is how the system evolves from time 0 to time 4, using the calculated feedback matrix , starting from the point x(0) = [1;1;1].
First solve the differential equation:
[Times, xvals] = ode45(@(u,x)((A + B*K*C)*x),[0,4],[1;1;1]);
Then plot the result:
plot(Times,xvals) legend('x_1(t)','x_2(t)','x_3(t)','Location','best') xlabel('t'); ylabel('x(t)');

Set Goals To Be Achieved Exactly
Suppose we now require the eigenvalues to be as near as possible to the goal values, [–5, –3, –1]. Set options.EqualityGoalCount to the number of objectives that should be as near as possible to the goals (i.e., do not try to over-achieve):
All three objectives should be as near as possible to the goals.
options.EqualityGoalCount = 3;
Call Optimization Solver
We are ready to call the optimization solver:
[K,fval,attainfactor,exitflag,output,lambda] = ...
fgoalattain(eigfun,K0,goal,weight,[],[],[],[],lb,ub,[],options); Attainment Max Line search Directional
Iter F-count factor constraint steplength derivative Procedure
0 6 0 1.88521
1 13 1.031 0.02998 1 0.745
2 20 0.3525 0.06863 1 -0.613
3 27 0.1528 -0.009105 1 -0.22 Hessian modified
4 34 0.02684 0.03722 1 -0.166 Hessian modified
5 41 1.041e-17 0.005702 1 -0.116 Hessian modified
6 48 1.459e-18 9.699e-06 1 -7.73e-16 Hessian modified
7 55 -5.082e-23 4.969e-11 1 -7.65e-14 Hessian modified
Local minimum possible. Constraints satisfied.
fgoalattain stopped because the size of the current search direction is less than
twice the value of the step size tolerance and constraints are
satisfied to within the value of the constraint tolerance.
<stopping criteria details>
The value of the control parameters at this solution is:
K
K = 2×2
-1.5954 1.2040
-0.4201 -2.9046
This time the eigenvalues of the closed loop system, which are also held in output fval, are as follows:
eigfun(K)
ans = 3×1
-5.0000
-3.0000
-1.0000
The attainment factor is the level of goal achievement. A negative attainment factor indicates over-achievement, positive indicates under-achievement. The low attainfactor obtained indicates that the eigenvalues have almost exactly met the goals:
attainfactor
attainfactor = -5.0824e-23
Evolution of New System Via Solution to ODE
Here is how the system evolves from time 0 to time 4, using the new calculated feedback matrix , starting from the point x(0) = [1;1;1].
First solve the differential equation:
[Times, xvals] = ode45(@(u,x)((A + B*K*C)*x),[0,4],[1;1;1]);
Then plot the result:
plot(Times,xvals) legend('x_1(t)','x_2(t)','x_3(t)','Location','best') xlabel('t'); ylabel('x(t)');