Simulating MPC Controller with Plant Model Mismatch
This example shows how to simulate a model predictive controller with a mismatch between the predictive plant model and the actual plant, as well as measured and unmeasured disturbances, using the sim command.
The predictive plant model has 2 manipulated variables, 2 unmeasured input disturbances, and 2 measured outputs. The actual plant has different dynamics.
Define Plant Model
Define the parameters of the nominal plant which the MPC controller is based on. Systems from MV to MO and UD to MO are identical.
p1 = tf(1,[1 2 1])*[1 1; 0 1]; plant = ss([p1 p1],'minimal'); plant.InputName = {'mv1','mv2','ud3','ud4'};
Design MPC Controller
Define inputs 1 and 2 as manipulated variables, 3 and 4 as unmeasured disturbances.
plant = setmpcsignals(plant,'MV',[1 2],'UD',[3 4]); % Create the controller object with sampling period, prediction and control % horizons: mpcobj = mpc(plant,1,40,2);
-->"Weights.ManipulatedVariables" is empty. Assuming default 0.00000. -->"Weights.ManipulatedVariablesRate" is empty. Assuming default 0.10000. -->"Weights.OutputVariables" is empty. Assuming default 1.00000.
For unmeasured input disturbances, the MPC controller will use the following unmeasured disturbance model.
distModel = eye(2,2)*ss(-.5,1,1,0); mpcobj.Model.Disturbance = distModel;
Define the Real Plant Model Used in Simulation
Define the parameters of the actual plant in closed loop with the MPC controller.
p2 = tf(1.5,[0.1 1 2 1])*[1 1; 0 1]; psim = ss([p2 p2],'minimal'); psim = setmpcsignals(psim,'MV',[1 2],'UD',[3 4]);
Simulate Closed-Loop Response Using the SIM Command
Define reference trajectories and unmeasured disturbances entering the actual plant.
dist = ones(1,2); % unmeasured disturbance signal refs = [1 2]; % output reference signal Tf = 20; % total number of simulation steps
Create an MPC simulation options object. This allows you to define both unmeasured disturbances and a plant different than the one which the MPC controller uses as a prediction model.
options = mpcsimopt(mpcobj); options.unmeas = dist; % unmeasured disturbance signal options.model = psim; % real plant model
Run the closed-loop MPC simulation with model mismatch and unforeseen unmeasured disturbance inputs.
sim(mpcobj,Tf,refs,options);
-->Converting model to discrete time. -->Assuming output disturbance added to measured output #1 is integrated white noise. -->Assuming output disturbance added to measured output #2 is integrated white noise. -->"Model.Noise" is empty. Assuming white noise on each measured output. -->Converting model to discrete time.
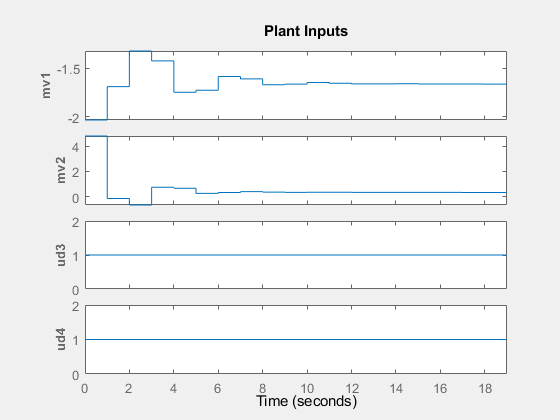

The closed loop tracking performance is acceptable despite the presence of model mismatches and unmeasured input disturbances.