Obstacle Avoidance Using Adaptive Model Predictive Control
This example shows how to make a vehicle (ego car) follow a reference velocity and avoid obstacles in the lane using adaptive MPC. To do so, you update the plant model and linear mixed input/output constraints at run time.
Obstacle Avoidance
A vehicle with obstacle avoidance (or passing assistance) has a sensor, such as lidar, that measures the distance to an obstacle in front of the vehicle and in the same lane. The obstacle can be static, such as a large pot hole, or moving, such as a slow-moving vehicle. The most common maneuver from the driver is to temporarily move to another lane, drive past the obstacle, and move back to the original lane.
As part of the autonomous driving experience, an obstacle avoidance system can perform the maneuver without human intervention. In this example, you design an obstacle avoidance system that moves the ego car around a static obstacle in the lane using throttle and steering angle. This system uses an adaptive model predictive controller that updates both the predictive model and the mixed input/output constraints at each control interval.
Vehicle Model
The ego car has a rectangular shape with a length of 5 meters and width of 2 meters. The model has four states:
 - Global X position of the car center
- Global X position of the car center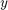 - Global Y position of the car center
- Global Y position of the car center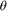 - Heading angle of the car (
- Heading angle of the car (0when facing east, counterclockwise positive) - Speed of the car (positive)
- Speed of the car (positive)
There are two manipulated variables:
 - Throttle (positive when accelerating, negative when decelerating)
- Throttle (positive when accelerating, negative when decelerating)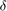 - Steering angle (0 when aligned with car, counterclockwise positive)
- Steering angle (0 when aligned with car, counterclockwise positive)
Use a simple nonlinear model to describe the dynamics of the ego car:
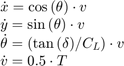
The analytical Jacobians of nonlinear state-space model are used to construct the linear prediction model at the nominal operating point.
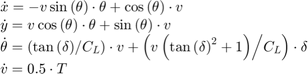
where  is the car length.
is the car length.
Assume all the states are measurable. At the nominal operating point, the ego car drives east at a constant speed of 20 meters per second.
V = 20; x0 = [0; 0; 0; V]; u0 = [0; 0];
Discretize the continuous-time model using the zero-order holder method in the obstacleVehicleModelDT function.
Ts = 0.02;
[Ad,Bd,Cd,Dd,U,Y,X,DX] = obstacleVehicleModelDT(Ts,x0,u0);
dsys = ss(Ad,Bd,Cd,Dd,Ts=Ts);
dsys.InputName = {'Throttle','Delta'};
dsys.StateName = {'X','Y','Theta','V'};
dsys.OutputName = dsys.StateName;
Road and Obstacle Information
In this example, assume that:
The road is straight and has three lanes.
Each lane is four meters wide.
The ego car drives in the middle of the center lane when not passing.
Without losing generality, the ego car passes an obstacle only from the left (fast) lane.
lanes = 3; laneWidth = 4;
The obstacle in this example is a nonmoving object in the middle of the center lane with the same size as the ego car.
obstacle = struct; obstacle.Length = 5; obstacle.Width = 2;
Place the obstacle 50 meters down the road.
obstacle.X = 50; obstacle.Y = 0;
Create a virtual safe zone around the obstacle so that the ego car does not get too close to the obstacle when passing it. The safe zone is centered on the obstacle and has a:
Length equal to two car lengths
Width equal to two lane widths
obstacle.safeDistanceX = obstacle.Length; obstacle.safeDistanceY = laneWidth; obstacle = obstacleGenerateObstacleGeometryInfo(obstacle);
In this example, assume that the lidar device can detect an obstacle 30 meters in front of the vehicle.
obstacle.DetectionDistance = 30;
Plot the following at the nominal condition:
Ego car - Green dot with black boundary
Horizontal lanes - Dashed blue lines
Obstacle - Red
xwith black boundarySafe zone - Dashed red boundary.
f = obstaclePlotInitialCondition(x0,obstacle,laneWidth,lanes);

MPC Design at the Nominal Operating Point
Design a model predictive controller that can make the ego car maintain a desired velocity and stay in the middle of the center lane.
status = mpcverbosity("off");
mpcobj = mpc(dsys);
The prediction horizon is 25 steps, which is equivalent to 0.5 seconds.
mpcobj.PredictionHorizon = 60;%25; mpcobj.ControlHorizon = 2;%5;
To prevent the ego car from accelerating or decelerating too quickly, add a hard constraint of 0.2 (m/s^2) on the throttle rate of change.
mpcobj.ManipulatedVariables(1).RateMin = -0.2*Ts; mpcobj.ManipulatedVariables(1).RateMax = 0.2*Ts;
Similarly, add a hard constraint of 6 degrees per second on the steering angle rate of change.
mpcobj.ManipulatedVariables(2).RateMin = -pi/30*Ts; mpcobj.ManipulatedVariables(2).RateMax = pi/30*Ts;
Scale the throttle and steering angle by their respective operating ranges.
mpcobj.ManipulatedVariables(1).ScaleFactor = 2; mpcobj.ManipulatedVariables(2).ScaleFactor = 0.2;
Since there are only two manipulated variables, to achieve zero steady-state offset, you can choose only two outputs for perfect tracking. In this example, choose the Y position and velocity by setting the weights of the other two outputs (X and theta) to zero. Doing so lets the values of these other outputs float.
mpcobj.Weights.OutputVariables = [0 30 0 1];
Update the controller with the nominal operating condition. For a discrete-time plant:
U = u0X = x0Y = Cd*x0 + Dd*u0DX = Ad*X0 + Bd*u0 - x0
mpcobj.Model.Nominal = struct(U=U,Y=Y,X=X,DX=DX);
Specify Mixed I/O Constraints for Obstacle Avoidance Maneuver
There are different strategies to make the ego car avoid an obstacle on the road. For example, a real-time path planner can compute a new path after an obstacle is detected and the controller follows this path.
In this example, use a different approach that takes advantage of the ability of MPC to handle constraints explicitly. When an obstacle is detected, it defines an area on the road (in terms of constraints) that the ego car must not enter during the prediction horizon. At the next control interval, the area is redefined based on the new positions of the ego car and obstacle until passing is completed.
To define the area to avoid, use the following mixed input/output constraints:
E*u + F*y <= G
where u is the manipulated variable vector and y is the output variable vector. You can update the constraint matrices E, F, and G when the controller is running.
The first constraint is an upper bound on 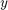 (
(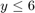 on this three-lane road).
on this three-lane road).
E1 = [0 0]; F1 = [0 1 0 0]; G1 = laneWidth*lanes/2;
The second constraint is a lower bound on 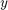 (
( on this three-lane road).
on this three-lane road).
E2 = [0 0]; F2 = [0 -1 0 0]; G2 = laneWidth*lanes/2;
The third constraint is for obstacle avoidance. Even though no obstacle is detected at the nominal operating condition, you must add a "fake" constraint here because you cannot change the dimensions of the constraint matrices at run time. For the fake constraint, use a constraint with the same form as the second constraint.
E3 = [0 0]; F3 = [0 -1 0 0]; G3 = laneWidth*lanes/2;
Specify the mixed input/output constraints in the controller using the setconstraint function.
setconstraint(mpcobj,[E1;E2;E3],[F1;F2;F3],[G1;G2;G3],[1;1;0.1]);
Simulate Controller
In this example, you use an adaptive MPC controller because it handles the nonlinear vehicle dynamics more effectively than a traditional MPC controller. A traditional MPC controller uses a constant plant model. However, adaptive MPC allows you to provide a new plant model at each control interval. Because the new model describes the plant dynamics more accurately at the new operating condition, an adaptive MPC controller performs better than a traditional MPC controller.
Also, to enable the controller to avoid the safe zone surrounding the obstacle, you update the third mixed constraint at each control interval. Basically, the ego car must be above the line formed from the ego car to the upper left corner of the safe zone. For more details, open obstacleComputeCustomConstraint.
Use a constant reference signal.
refSignal = [0 0 0 V];
Initialize plant and controller states.
x = x0; u = u0; egoStates = mpcstate(mpcobj);
The simulation time is 4 seconds.
T = 0:Ts:4;
Log simulation data for plotting.
saveSlope = zeros(length(T),1); saveIntercept = zeros(length(T),1); ympc = zeros(length(T),size(Cd,1)); umpc = zeros(length(T),size(Bd,2));
Run the simulation.
for k = 1:length(T) % Obtain new plant model and output measurements for interval |k|. [Ad,Bd,Cd,Dd,U,Y,X,DX] = obstacleVehicleModelDT(Ts,x,u); measurements = Cd * x + Dd * u; ympc(k,:) = measurements'; % Determine whether the vehicle sees the obstacle, and update the mixed % I/O constraints when obstacle is detected. detection = obstacleDetect(x,obstacle,laneWidth); [E,F,G,saveSlope(k),saveIntercept(k)] = ... obstacleComputeCustomConstraint(x,detection,obstacle,laneWidth,lanes); % Prepare new plant model and nominal conditions for adaptive MPC. newPlant = ss(Ad,Bd,Cd,Dd,Ts=Ts); newNominal = struct(U=U,Y=Y,X=X,DX=DX); % Prepare new mixed I/O constraints. options = mpcmoveopt; options.CustomConstraint = struct(E=E,F=F,G=G); % Compute optimal moves using the updated plant, nominal conditions, % and constraints. [u,Info] = mpcmoveAdaptive(mpcobj,egoStates,newPlant,newNominal,... measurements,refSignal,[],options); umpc(k,:) = u'; % Update the plant state for the next iteration |k+1|. x = Ad * x + Bd * u; end mpcverbosity(status);
Analyze Results
Plot the trajectory of the ego car (black line) and the third mixed I/O constraints (dashed green lines) during the obstacle avoidance maneuver.
figure(f) for k = 1:length(saveSlope) X = [0;50;100]; Y = saveSlope(k)*X + saveIntercept(k); line(X,Y,LineStyle="--",Color="g") end plot(ympc(:,1),ympc(:,2),"-k"); axis([0 ympc(end,1) -laneWidth*lanes/2 laneWidth*lanes/2]) % reset axis

The MPC controller successfully completes the task without human intervention.
Simulate Controller in Simulink
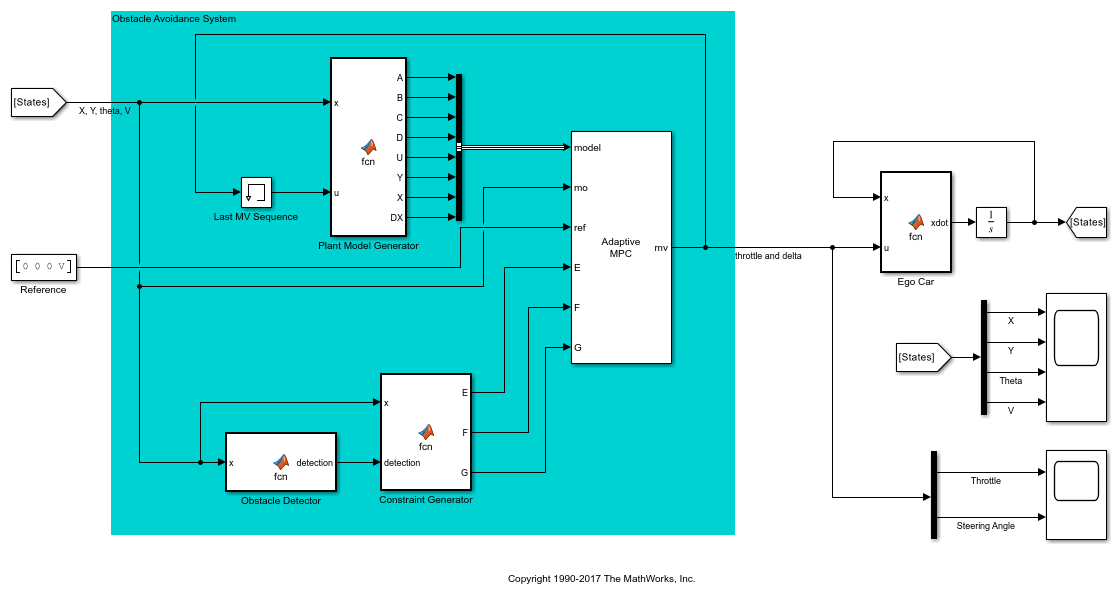
Open the Simulink® model. The obstacle avoidance system contains multiple components:
Plant Model Generator: Produce new plant model and nominal values.
Obstacle Detector: Detect obstacle (lidar sensor not included).
Constraint Generator: Produce new mixed I/O constraints.
Adaptive MPC: Control obstacle avoidance maneuver.
mdl = "mpc_ObstacleAvoidance";
open_system(mdl)
sim(mdl)

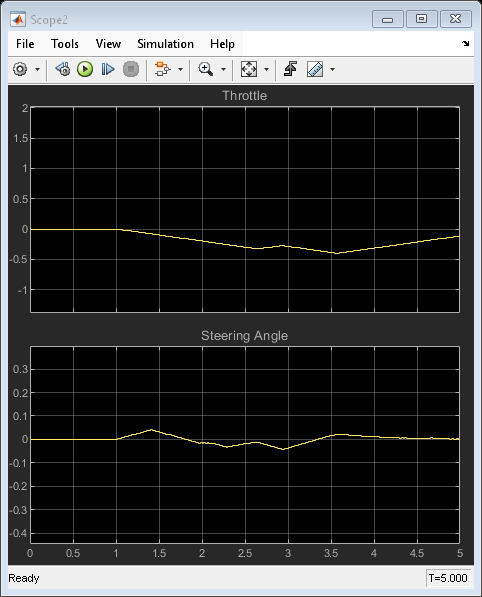
The simulation result is identical to the command-line result. To support a rapid prototyping workflow, you can generate C/C++ code for the blocks in the obstacle avoidance system.
bdclose(mdl)
See Also
Functions
Objects
mpc|mpcstate|mpcmoveopt