Page-Wise Matrix Functions

If you use for-loops for repetitive matrix operations on N-D arrays, consider simplifying your code with page-wise matrix functions. These functions make operations involving N-D arrays, which are containers for dense matrices, easier to write and faster to run.

Simplifying Code for Matrix Operations on N-D Arrays

For example, compute array C as a collection of matrices formed by multiplying the matrices contained in the first two dimensions of 3-D arrays A and B.

You can multiply the corresponding matrices by writing a for-loop. For this example, create A and B as sets of 100,000 matrices of random numbers. A contains 3-by-4 matrices, and B contains 4-by-2 matrices. Multiply each pair of corresponding matrices to form the array C, which contains 100,000 matrices of size 3-by-2.

A = rand(3,4,100000);
B = rand(4,2,100000);
loopC = zeros(3,2,100000);
tic 
for i=1:100000
    loopC(:,:,i) = A(:,:,i) * B(:,:,i);
end
toc

Elapsed time is 0.165887 seconds.

Using the page-wise matrix function pagemtimes, you can simplify the code for this operation.

tic
pageC = pagemtimes(A,B);
toc

Elapsed time is 0.020894 seconds.

Compare the results obtained with these approaches. The resulting arrays are the same.

isequal(pageC,loopC)

ans = logical
   1

How Do Page-Wise Matrix Functions Work?

Page-wise functions operate on 2-D matrices that have been arranged into a multidimensional array. For example, the elements in the third dimension of a 3-D array are commonly called pages because they stack on top of each other like pages in a book. Each page is a matrix that the function operates on.

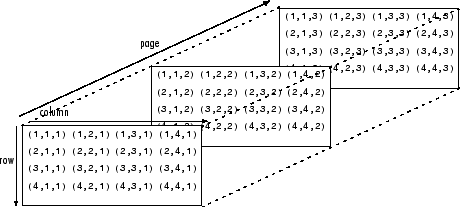
You can also assemble a collection of 2-D matrices into a higher dimensional array, like a 4-D or 5-D array, and in these cases, a page-wise function still treats the fundamental unit of the array as a 2-D matrix that the function operates on, such as X(:,:,i,j,k,l). The cat function is useful for assembling a collection of matrices into a multidimensional array, and the zeros function is useful for preallocating a multidimensional array.

Page-Wise Matrix Functions Available in MATLAB®

MATLAB provides a growing list of page-wise matrix functions. The current list includes functions for page-wise left and right matrix division, matrix inversion, transposition, singular value decomposition, matrix norm, and calculation eigenvalues and eigenvectors. For the complete list, expand the Page-wise Matrix Functions section under "Functions" on the Linear Algebra page.

Typically, the page-wise versions of functions have the same name as the standard 2-D matrix functions, but with the prefix page. For instance, the svd function performs the singular value decomposition, the pagesvd function performs the page-wise singular value decomposition of the matrices in an N-D array.

For example, create two 4-by-4 matrices and concatenate them along the third dimension into a 4-by-4-by-2 array.

A = magic(4);
B = hilb(4);
X = cat(3,A,B);

Calculate the singular values of each page of X by using pagesvd.

S = pagesvd(X)

S = 
S(:,:,1) =

   34.0000
   17.8885
    4.4721
    0.0000


S(:,:,2) =

    1.5002
    0.1691
    0.0067
    0.0001

If you compute the singular values of matrices A and B by using the svd function, you get the same results.

svd(A)

ans = 4×1

   34.0000
   17.8885
    4.4721
    0.0000

svd(B)

ans = 4×1

    1.5002
    0.1691
    0.0067
    0.0001

Performance Gains

In general, page-wise matrix functions are easier to write and faster to run than the equivalent for-loop approach. For example, find the eigenvalues for a set of 1000 square matrices of random numbers by using the for-loop approach and the pageeig function.

Compare the computation times for these two approaches using different matrix sizes. For this example, vary the size of the matrix from 2 to 100.

matrixSizes = [2 5 10:10:100];

Create vectors for storing for-loop and pageeig computation times for each matrix size.

n = numel(matrixSizes);
tLoop = zeros(n,1);
tPage = zeros(n,1);

Create a function that computes the eigenvalues by using the for-loop approach.

function Bloop = loopeig(A)
m = size(A,1);
p = size(A,3);
Bloop = zeros(m,1,p);
for j = 1:p
    Bloop(:,:,j) = eig(A(:,:,j));
end
end

Compute the eigenvalues of each matrix from the set of 1000 matrices by using the for-loop approach and the pageeig function. Store the computation times in vectors tLoop and tPage.

rng("default"); % for reproducibility
for i = 1:n
    m = matrixSizes(i);
    A = rand(m,m,1000);
    f = @() loopeig(A);
    tLoop(i) = timeit(f);
    f = @() pageeig(A);
    tPage(i) = timeit(f);
end

Plot the times and the speed-up factors for various numbers of rows.

function plotTimes(matrixSizes,tPage,tLoop)
figure(Position=[100,100,1200,450])
t = tiledlayout(1,2);

nexttile
plot(matrixSizes,tPage,"*")
hold on
plot(matrixSizes,tLoop,"o")
legend({"pageeig","for-loop"},Location="northwest")
title("Times")
xlabel("Matrix Size")
ylabel("Seconds")
hold off

nexttile
plot(matrixSizes,tLoop./tPage)
title("Speed-ups of pageeig over for-loop")
xlabel("Matrix Size")
end

plotTimes(matrixSizes,tPage,tLoop)

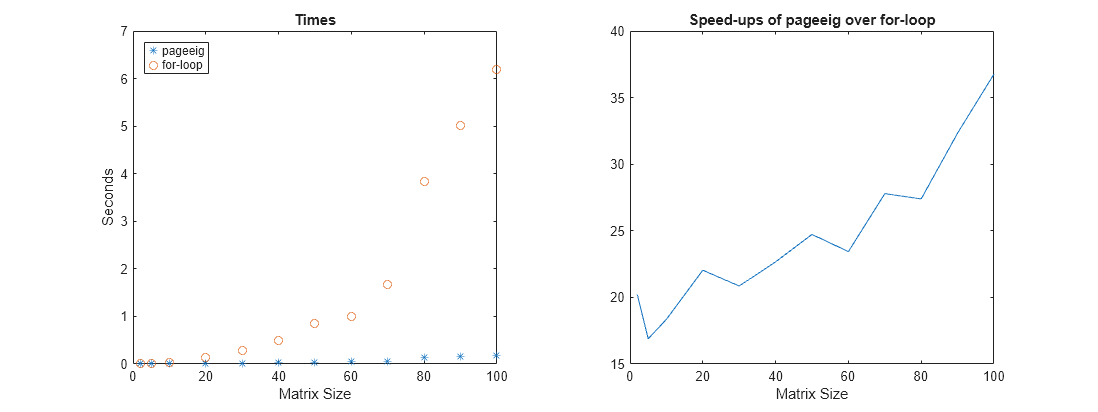
The first plot shows that the for-loop approach takes more time than pageeig. The second plot shows that the benefit of using pageeig is largest when there are many small matrices. However, even for the larger matrices, the speed-up factor is substantial. The page-wise functions are typically faster than the for-loop approach for these reasons:

• Argument checking. With the page-wise functions, you check arguments only once. If you loop over 1000 pages, you check arguments 1000 times. The improvement for smaller matrices is more significant because the argument-checking overhead makes up a larger percentage of the overall time. For larger matrices, this overhead can be insignificant. With thousands of very small matrices, the time for argument-checking can be comparable to the computation time.

• More parallelism. Most of the linear algebra functions in MATLAB already run in parallel. To see evidence of this behavior, multiply two large matrices and monitor your CPU workload. However, when you loop over many pages containing small matrices, the individual function call is too quick to benefit from running in parallel, and the loop itself runs the iterations sequentially. Page-wise matrix functions do not have this limitation: operations on small matrices (pages) in a set can be executed at the same time. Depending on the linear algebra operation and the specified set of matrices, MATLAB page-wise matrix functions choose the threading approach that seems to be more beneficial for the particular case, by choosing between threading per page or sequential execution per page but threading across the whole set of pages.