Structuring Elements
An essential part of the morphological dilation and erosion operations is the structuring element used to probe the input image. A structuring element is a matrix that defines the neighborhood used to process each pixel in the image. The center pixel of the structuring element, called the origin, identifies the pixel in the image being processed.
You typically choose a structuring element of the same size and shape as the objects you want to process in the input image. For example, to find lines in an image, create a linear structuring element.
There are two types of structuring elements: flat and
nonflat. A flat structuring element is a binary valued
neighborhood, either 2-D or multidimensional, in which the true
(1-valued) pixels are included in the morphological operation,
and the false (0-valued) pixels are not. Use the
strel function to create a flat
structuring element. You can use flat structuring elements with both binary and
grayscale images. The following figure illustrates a flat structuring element.

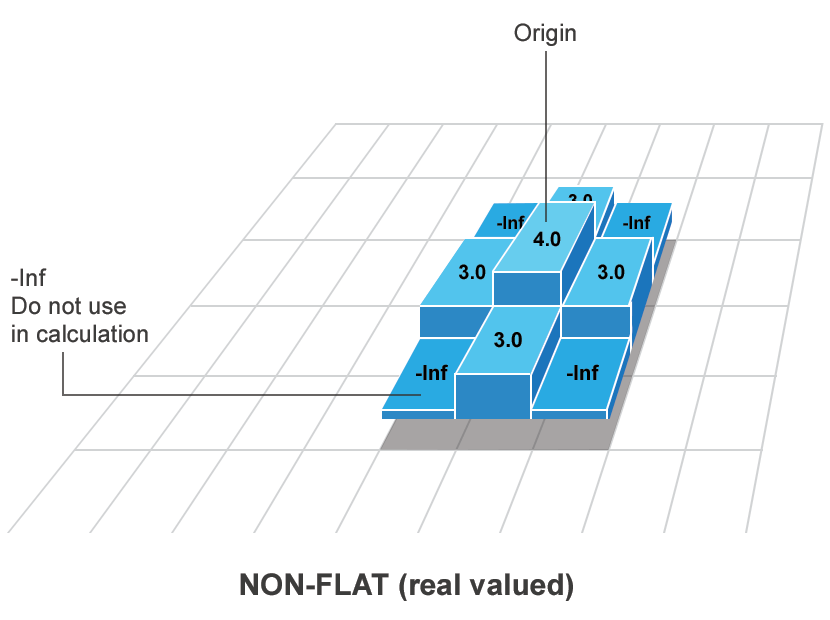
You can use nonflat structuring elements only with grayscale images. A nonflat
structuring element includes an additive offset for each pixel in the neighborhood.
Pixels in the neighborhood that have a finite real value are used in the morphological
operation. Pixels in the neighborhood with the value -Inf are not
used in the operation. Use the offsetstrel function to create a nonflat
structuring element.
Determine the Origin of a Structuring Element
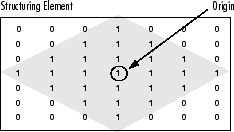
The morphological functions use this code to get the coordinates of the origin of structuring elements of any size and dimension:
origin = floor((size(nhood)+1)/2)
where nhood is the neighborhood defining the structuring
element. To see the neighborhood of a flat structuring element, view the
Neighborhood property of the strel object.
To see the neighborhood of a nonflat structuring element, view the
Offset property of the offsetstrel
object.
For example, the following illustrates the origin of a flat, diamond-shaped structuring element.
Structuring Element Decomposition
To enhance performance, the strel and offsetstrel functions might break
structuring elements into smaller pieces, a technique known as structuring
element decomposition.
For example, dilation by an 11-by-11 square structuring element can be accomplished by dilating first with a 1-by-11 structuring element, and then with an 11-by-1 structuring element. This results in a theoretical speed improvement of a factor of 5.5, although in practice the actual speed improvement is somewhat less.
Structuring element decompositions used for the "disk" and
"ball" shapes are approximations; all other decompositions
are exact. Decomposition is not used with an arbitrary structuring element unless it
is a flat structuring element whose neighborhood matrix is all
1's.
To see the sequence of structuring elements used in a decomposition, use the
decompose method. Both strel objects and
offsetstrel objects support decompose methods. The
decompose method returns an array of the structuring elements
that form the decomposition. For example, here are the structuring elements created
in the decomposition of a diamond-shaped structuring element.
SE = strel("diamond",4)
SE =
strel is a diamond shaped structuring element with properties:
Neighborhood: [9x9 logical]
Dimensionality: 2Call the decompose method. The method returns an array of structuring elements.
decompose(SE)
ans =
3x1 strel array with properties:
Neighborhood
Dimensionality