Elbow (TL)
Libraries:
Simscape /
Fluids /
Isothermal Liquid /
Pipes & Fittings
Description
The Elbow (TL) block represents flow in a pipe turn in a thermal liquid network. Pressure losses due to pipe turns are calculated, but the block omits the effects of viscous friction.
Two Elbow type settings are available:
Smoothly-curved and Sharp-edged
(Miter). For a smooth pipe with a 90° bend and losses due to friction,
you can also use the Pipe Bend (TL) block.
Loss Coefficients
When the Elbow type parameter is Smoothly
curved, the block calculates the loss coefficient as:
The block calculates Cangle, the angle correction factor, from Keller [2] as
where θ is the value of the Bend angle parameter in degrees. The block defines the friction factor, fT, as the value for clean commercial steel. The block then interpolates the values from tabular data based on the internal elbow diameter for fT based on Crane [1]. This table contains the pipe friction data for clean commercial steel pipe with flow in the zone of complete turbulence.
| r/d | 1 | 1.5 | 2 | 3 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 20 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| K | 20 fT | 14 fT | 12 fT | 12 fT | 14 fT | 17 fT | 24 fT | 30 fT | 34 fT | 38 fT | 42 fT | 50 fT | 58 fT |
The values from Crane are valid for diameters up to 600 millimeters. The friction factor for larger diameters or for wall roughness beyond this range is calculated by nearest-neighbor extrapolation.
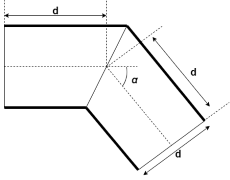
When the Elbow type parameter is Sharp-edged
(Miter), the block calculates the loss coefficient
K for the bend angle, α, according to
Crane [1].
| α | 0° | 15° | 30° | 45° | 60° | 75° | 90° |
|---|---|---|---|---|---|---|---|
| K | 2 fT | 4 fT | 8 fT | 15 fT | 25 fT | 40 fT | 60 fT |
Mass Flow Rate
Mass is conserved through the pipe segment:
The mass flow rate through the elbow is calculated as:
where:
A is the flow area.
is the average fluid density.
Δp is the pipe segment pressure difference, pA – pB.
The critical pressure difference, Δpcrit, is the pressure differential associated with the Critical Reynolds number, Recrit, the flow regime transition point between laminar and turbulent flow:
where
ν is the fluid kinematic viscosity.
D is the elbow internal diameter.
Energy Balance
The block balances energy such that
where:
ϕA is the energy flow rate at port A.
ϕB is the energy flow rate at port B.
Ports
Conserving
Parameters
References
[1] Crane Co. Flow of Fluids Through Valves, Fittings, and Pipe TP-410. Crane Co., 1981.
[2] Keller, G. R. Hydraulic System Analysis. Penton, 1985.
Extended Capabilities
Version History
Introduced in R2022a
