Getting Started with HDL Coder Native Floating-Point Support
Native floating-point support in HDL Coder™ enables you to generate code from your floating-point design. If your design has complex math and trigonometric operations or has data with a large dynamic range, use native floating point. You can use native floating point with a Simulink® model or a MATLAB® function.
Key Features
In your Simulink model or MATLAB function:
You can have half-precision, single-precision, and double-precision floating-point data types and operations.
You can have a combination of integer, fixed-point, and floating-point operations. By using Data Type Conversion blocks, you can perform conversions between floating-point and fixed-point data types.
The generated code:
Complies with the IEEE® 754 standard of floating-point arithmetic.
Is target-independent. You can deploy the code on any generic FPGA or an ASIC.
Does not require floating-point processing units or hard floating-point DSP blocks on the target ASIC or FPGA.
HDL Coder supports:
Math and trigonometric functions
Large subset of Simulink blocks
Denormal numbers
Customizing the latency of the floating-point operator
Numeric Considerations and IEEE 754 Standard Compliance
Native floating point technology in HDL Coder adheres to the IEEE standard of floating-point arithmetic. For basic arithmetic operations such as addition, subtraction, multiplication, division, and reciprocal, when you generate HDL code in native floating-point mode, the numeric results obtained match the original Simulink model or MATLAB function.
Certain advanced math operations such as exponential, logarithm, and trigonometric operators have machine-specific implementation behaviors because these operators use recurring Taylor series and Remez expression based implementations. When you use these operators in native floating-point mode, the generated HDL code can have relatively small numeric differences from the Simulink model or MATLAB function. These numeric differences are within a tolerance range and are compliant with the IEEE 754 standard.
To generate code that complies with the IEEE 754 standard, HDL Coder supports:
Round to nearest rounding mode
Denormal numbers
Exceptions such as NaN (Not a Number), Inf, and Zero
Customization of ULP (Units in the Last Place) and relative accuracy
For more information, see Numeric Considerations for Native Floating-Point.
Floating Point Types
Single Precision
In the IEEE 754–2008 standard, the single-precision floating-point number is 32 bits. The 32-bit number encodes a 1-bit sign, an 8-bit exponent, and a 23-bit mantissa.
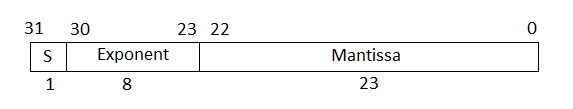
This graph is the normalized representation for floating-point numbers. You can compute the actual value of a normal number as:
The exponent field represents the exponent plus a bias of 127. The size of the mantissa is 24 bits. The leading bit is a 1, so the representation encodes the lower 23 bits.
Use single-precision types for applications that require larger dynamic range than half-precision types. Single-precision operations consume less memory and has lower latency than double-precision types.
Double Precision
In the IEEE 754–2008 standard, the double-precision floating-point number is 64 bits. The 64-bit number encodes a 1-bit sign, an 11-bit exponent, and a 52-bit mantissa.
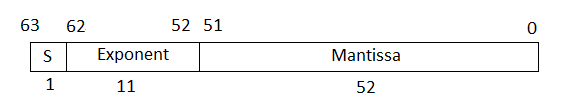
The exponent field represents the exponent plus a bias of 1023. The size of the mantissa is 53 bits. The leading bit is a 1, so the representation encodes the lower 52 bits.
Use double-precision types for applications that require larger dynamic range, accuracy, and precision. These operations consume larger area on the FPGA and lower target frequency.
Half Precision
In the IEEE 754–2008 standard, the half-precision floating-point number is 16 bits. The 16-bit number encodes a 1-bit sign, a 5-bit exponent, and a 10-bit mantissa.
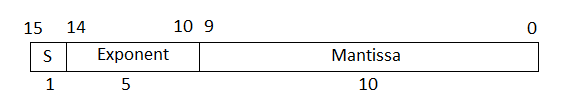
The exponent field represents the exponent plus a bias of 15. The size of the mantissa is 11 bits. The leading bit is a 1, so the representation encodes the lower 10 bits.
Use half-precision types for applications that require smaller dynamic range, consumes much less memory, has lower latency, and saves FPGA resources.
When using half types, you might want to explicitly set the
Output data type of the blocks to half instead
of the default setting Inherit: Inherit via internal rule. To
learn how to change the parameters programmatically, see Set HDL Block Parameters for Multiple Blocks Programmatically.
Data Type Considerations
With native floating-point support, HDL Coder supports code generation from Simulink models or MATLAB functions that contain floating-point signals and fixed-point signals. You can model your design with floating-point types to:
Implement algorithms that have a large or unknown dynamic range that can fall outside the range of representable fixed-point types.
Implement complex math and trigonometric operations that are difficult to design in fixed point.
Obtain a higher precision and better accuracy.
Floating-point designs can potentially occupy more area on the target hardware. In your
Simulink model or MATLAB function, it is recommended to use floating-point data types in the algorithm
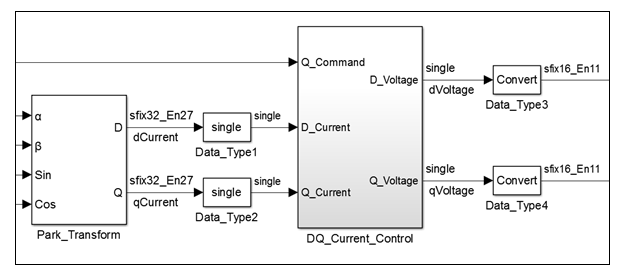
data path and fixed-point data types in the algorithm control logic. This figure shows a
section of a Simulink model that uses single and fixed-point types. By using
Data Type Conversion blocks, you can perform conversions between the single
and fixed-point types.