Effects of Pattern Search Options, Problem-Based
This example shows the effects of some options for pattern search in the problem-based approach. The options include plotting, stopping criteria, and other algorithmic controls for speeding a solution. For a list of available options for patternsearch algorithms, see Options Table for Pattern Search Algorithms.
Set Up a Problem for Pattern Search
The problem to minimize is a quadratic function of six variables subject to linear equality and inequality constraints. The objective function, lincontest7, is available when you run this example.
type lincontest7function y = lincontest7(x)
%LINCONTEST7 objective function.
% y = LINCONTEST7(X) evaluates y for the input X. Make sure that x is a column
% vector, whereas objective function gets a row vector.
% Copyright 2003-2017 The MathWorks, Inc.
x = x(:);
%Define a quadratic problem in terms of H and f
H = [36 17 19 12 8 15;
17 33 18 11 7 14;
19 18 43 13 8 16;
12 11 13 18 6 11;
8 7 8 6 9 8;
15 14 16 11 8 29];
f = [ 20 15 21 18 29 24 ]';
y = 0.5*x'*H*x + f'*x;
Create a six-element optimization variable x as a row vector.
x = optimvar("x",1,6);Create an optimization problem with the objective function lincontest7(x).
prob = optimproblem("Objective",lincontest7(x));Specify an initial point for the optimization.
x0.x = [2 1 0 9 1 0];
Create linear constraint matrices for the constraints Aineq*x' <= Bineq and Aeq*x' = Beq. You need to use x' in these constraints because x is a row vector.
Aineq = [-8 7 3 -4 9 0 ]; Bineq = [7]; Aeq = [7 1 8 3 3 3; 5 0 5 1 5 8; 2 6 7 1 1 8; 1 0 0 0 0 0]; Beq = [84 62 65 1]'; prob.Constraints.Aineq = Aineq*x' <= Bineq; prob.Constraints.Aeq = Aeq*x' == Beq;
Run the patternsearch solver, and note the number of iterations and function evaluations required to reach the solution.
[sol,Fval,eflag,output] = solve(prob,x0,"Solver","patternsearch");
Solving problem using patternsearch. patternsearch stopped because the mesh size was less than options.MeshTolerance.
fprintf('The number of iterations is: %d\n', output.iterations);The number of iterations is: 76
fprintf('The number of function evaluations is: %d\n', output.funccount);The number of function evaluations is: 709
fprintf('The best function value found is: %g\n', Fval);The best function value found is: 2189.18
Add Visualization
Monitor the optimization process by specifying options that select two plot functions. The plot function psplotbestf plots the best objective function value at every iteration, and the plot function psplotfuncount plots the number of times the objective function is evaluated at each iteration. Set these two plot functions in a cell array.
opts = optimoptions(@patternsearch,"PlotFcn",{@psplotbestf,@psplotfuncount});Run the patternsearch solver, including the opts argument.
[sol2,Fval2,eflag2,output2] = solve(prob,x0,"Solver","patternsearch",... "Options",opts);
Solving problem using patternsearch. patternsearch stopped because the mesh size was less than options.MeshTolerance.

Mesh Options
Pattern search involves evaluating the objective function at points in a mesh. The size of the mesh can influence the speed of the solution. You can control the size of the mesh by setting options.
Initial Mesh Size
The mesh at each iteration is the span of a set of search directions that are added to the current point, scaled by the current mesh size. The solver starts with an initial mesh size of 1 by default. To start with the initial mesh size of 1/2, set the InitialMeshSize option. This can save an iteration and several function evaluations when the initial point is good relative to a mesh of size 1.
opts = optimoptions(opts,'InitialMeshSize',1/2);Mesh Scaling
You can scale the mesh to improve the minimization of a poorly scaled optimization problem. Scaling rotates the pattern by some degree and scales along the search directions. The ScaleMesh option is on (true) by default, but you can turn it off if the problem is well scaled. In general, if the problem is poorly scaled, setting this option to true can reduce the number of function evaluations. For this problem, set ScaleMesh to false, because lincontest7 is a well-scaled objective function.
opts = optimoptions(opts,'ScaleMesh',false);Mesh Accelerator
Direct search methods require many function evaluations compared to derivative-based optimization methods. The pattern search algorithm can quickly find the neighborhood of an optimum point, but can be slow in detecting the minimum itself. The patternsearch solver can reduce the number of function evaluations by using an accelerator. When the accelerator is on (opts.AccelerateMesh = true), the solver contracts the mesh size rapidly after reaching a minimum mesh size. This option is recommended only for smooth problems; in other types of problems, you can lose some accuracy. The AccelerateMesh option is off (false) by default. For this problem, set AccelerateMesh to true because the objective function is smooth.
opts = optimoptions(opts,'AccelerateMesh',true);Run the patternsearch solver.
[sol3,Fval3,eflag3,output3] = solve(prob,x0,"Solver","patternsearch",... "Options",opts);
Solving problem using patternsearch. patternsearch stopped because the mesh size was less than options.MeshTolerance.
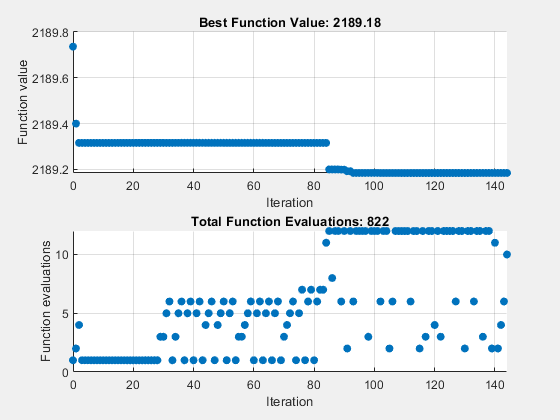
fprintf('The number of iterations is: %d\n', output3.iterations);The number of iterations is: 144
fprintf('The number of function evaluations is: %d\n', output3.funccount);The number of function evaluations is: 753
fprintf('The best function value found is: %g\n', Fval3);The best function value found is: 2189.18
The mesh option settings reduce the number of iterations and the number of function evaluations, and with no apparent loss of accuracy.
Stopping Criteria and Tolerances
MeshTolerance is a tolerance on the mesh size. If the mesh size is less than MeshTolerance, the solver stops. StepTolerance is the minimum tolerance on the change in the current point to the next point. FunctionTolerance is the minimum tolerance on the change in the function value from the current point to the next point.
Set the MeshTolerance to 1e-7, which is 10 times smaller than the default value. This setting can increase the number of function evaluations and iterations, and can lead to a more accurate solution.
opts.MeshTolerance = 1e-7;
Search Methods in Pattern Search
The pattern search algorithm can use an additional search method at every iteration, based on the value of the SearchFcn option. When you specify a search method using SearchFcn, patternsearch performs the specified search first, before the mesh search. If the search method is successful, patternsearch skips the mesh search, commonly called the poll function, for that iteration. If the search method is unsuccessful in improving the current point, patternsearch performs the mesh search.
You can specify different search methods for SearchFcn, including searchga and searchneldermead, which are optimization algorithms. Use these two search methods only for the first iteration, which is the default setting. Using either of these methods at every iteration might not improve the results and can be computationally expensive. However, you can use the searchlhs method, which generates Latin hypercube points, at every iteration or possibly every 10 iterations.
Other choices for search methods include poll methods such as positive basis N+1 or positive basis 2N. A recommended strategy is to use positive basis N+1 (which requires at most N+1 points to create a pattern) as a search method and positive basis 2N (which requires 2N points to create a pattern) as a poll method.
Update the options structure to use positivebasisnp1 as the search method. Because positive basis 2N is the default for the PollFcn option, do not set that option.
opts.SearchFcn = @positivebasisnp1;
Run the patternsearch solver.
[sol4,Fval4,eflag4,output4] = solve(prob,x0,"Solver","patternsearch",... "Options",opts);
Solving problem using patternsearch. patternsearch stopped because the mesh size was less than options.MeshTolerance.
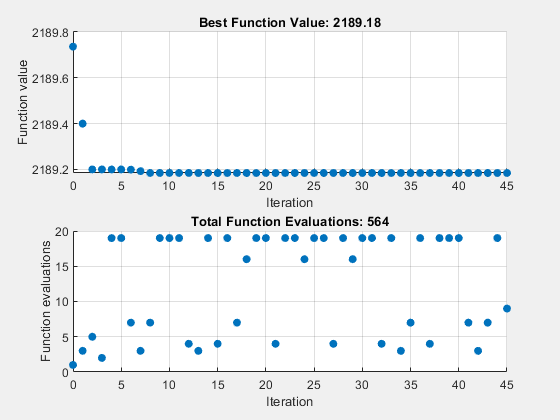
fprintf('The number of iterations is: %d\n', output4.iterations);The number of iterations is: 48
fprintf('The number of function evaluations is: %d\n', output4.funccount);The number of function evaluations is: 605
fprintf('The best function value found is: %g\n', Fval4);The best function value found is: 2189.18
The total number of iterations and function evaluations decreases, even though the mesh tolerance is smaller than its previous value and is the stopping criterion that halts the solver.