Tracking Using Bistatic Range Detections
This example shows you how to simulate bistatic range-only detections using four sensor-emitter pairs. In addition, this example demonstrates how to localize and track multiple targets using bistatic range-only measurements.
Introduction
A bistatic radar is a collection of a bistatic emitter or transmitter (![]() ), and a bistatic receiver or sensor (
), and a bistatic receiver or sensor (![]() ). The geometry of a bistatic system is depicted in the figure below. The sensor receives signals along the path forming the upper sides of the triangle
). The geometry of a bistatic system is depicted in the figure below. The sensor receives signals along the path forming the upper sides of the triangle ![]() with bistatic detections referenced to the emitter range. The relative bistatic range is given by:
with bistatic detections referenced to the emitter range. The relative bistatic range is given by:
![]()
where ![]() is the range from the emitter to the target,
is the range from the emitter to the target, ![]() is the range from the target to the sensor, and
is the range from the target to the sensor, and ![]() , known also as the direct-path or baseline, is the range from the emitter to the sensor.
, known also as the direct-path or baseline, is the range from the emitter to the sensor.

The emitter-to-target-to-sensor range obtained by the bistatic radar is equal to the sum:
![]()
This sum defines an ellipsoid of constant range. The image shown above describes the ellipsoid when target, transmitter and sensor lie in the same plane. This results in a 2-D ellipse. The target lies somewhere on the surface of the constant-range ellipsoid with the foci being the emitter and sensor locations, which are separated by the baseline distance L and with a major axis equal to 2a.
Next, you will define a scenario to generate the bistatic detections and then use the detections to track the targets.
Define Scenario
You define a tracking scenario which simulates the 3-D area containing multiple platforms. You will define the bistatic system in this scenario.
% Set the random seed for repeatable results. rng(2050); % Create a tracking scenario to manage the movement of platforms. scene = trackingScenario; % Set the duration of the scenario to 30 seconds and the update rate of the % scenario to 1 Hz. scene.StopTime = 30; % sec scene.UpdateRate = 1; % Hz
Set the number of each type of platform. In this example, the following types of platform will be created for sensing the targets:
1 radar emitter
4 bistatic radar sensors
% Set the minimum number of sensor-emitter pairs required by the spherical % intersection algorithm for a better localization of the targets in % 3-dimensional space. numSensors = 4; emitterIdx = 1; % Emitter is added as first platform in scene
Create and mount emitter
In a bistatic system, there are three types of emitters:
Dedicated: This type of transmitter is intentionally designed and operated to support bistatic processing.
Cooperative: This type of transmitter is designed to support other functions but is suitable for bistatic use. Information about the transmitter such as its transmitted waveform and position are known.
Non-Cooperative: This type is a "transmitter of opportunity". Non-cooperative transmitters cannot be controlled but are deemed suitable for bistatic use.
In this example, the modeled emitter is considered to be a dedicated transmitter. Model an RF emission using radarEmitter. This emitter is an ideal, isotropic emitter with a 360 degrees field of view. The waveform type is a user-defined value used to enumerate the various waveform types that are present in the scenario. For this scenario, use the value 1 to indicate an LFM type waveform. Mount the emitter to a stationary platform at the origin.
% Define an emitter. emitter = radarEmitter(emitterIdx,'No scanning', ... 'FieldOfView',[360 180], ... % [az el] deg 'CenterFrequency', 300e6, ... % Hz 'Bandwidth', 30e6, ... % Hz 'WaveformType', 1); % Use 1 for an LFM-like waveform % Mount emitter on a platform. thisPlat = platform(scene,'Trajectory',kinematicTrajectory('Position',[0 0 0],... 'Velocity',[0 0 0])); thisPlat.Emitters = {emitter};
Create and mount bistatic radar sensors
Model a bistatic radar sensor using radarSensor. The radar sensor is an ideal, isotropic receiver with a 360 degrees field of view. Set the DetectionMode to bistatic. Ensure that the sensor is configured so that its center frequency, bandwidth, and expected waveform types will match the emitter configuration. Enable INS for tracking in scenario coordinates and mount the bistatic radar sensor to platforms.
% Define some random trajectories for the four bistatic radar sensors. % Circularly distributed with some variance. r = 2000; % Range, m theta = linspace(0,pi,numSensors); % Theta, rad xSen = r*cos(theta) + 100*randn(1,numSensors); % m ySen = r*sin(theta) + 100*randn(1,numSensors); % m % To observe the z of the targets, the sensors must have some elevation % with respect to each other and emitter. zSen = -1000*rand(1,numSensors); % m % Define a bistatic radar sensor. sensor = fusionRadarSensor(1,'No scanning', ... 'FieldOfView',[360 180], ... % [az el] deg 'DetectionMode','Bistatic', ... % Bistatic detection mode 'CenterFrequency', 300e6, ... % Hz 'Bandwidth', 30e6, ... % Hz 'WaveformTypes', 1,... % Use 1 for an LFM-like waveform 'HasINS',true,... % Has INS to enable tracking in scenario 'AzimuthResolution',360,... % Does not measure azimuth and has a single resolution cell 'HasElevation',true,... % Enable elevation to set elevation resolution 'ElevationResolution',180); % Single elevation resolution cell % Mount bistatic radar sensors on platforms. for iD = 1:numSensors % Create a platform with the trajectory. The sensing platforms are % considered stationary, but can be provided with a velocity. thisPlat = platform(scene,... 'Trajectory',kinematicTrajectory('Position',[xSen(iD) ySen(iD) zSen(iD)],... 'Velocity',[0 0 0])); % Clone the bistatic radar sensor and mount to platforms. thisPlat.Sensors = {clone(sensor)}; % Provide the correct sensor index. thisPlat.Sensors{1}.SensorIndex = iD; end
Simulating the bistatic scenario involves the following:
Generating RF emissions
Propagating the emissions and reflecting these emissions from platforms
Receiving the emissions, calculating interference losses, and generating detections.
This process is wrapped in a supporting function, detectBistaticTargetRange, defined at the end of this example.
Target Localization
The figure in the Introduction section illustrated that with a bistatic measurement, the target lies somewhere on an ellipsoid defined by the emitter and sensor positions, as well as the measured bistatic range. Since the target can lie anywhere on the ellipsoid, a single bistatic measurement does not provide full observability of the target state. To localize the target (triangulate the target position) and achieve observability of target's state, multiple measurements from different sensors are needed. The target localization algorithm that is implemented in this example is based on the spherical intersection method described in reference [1]. The non-linear nature of the localization problem results in two possible target locations from intersection of 3 or more sensor bistatic ranges. A decision about target location from two possible locations can be facilitated by using more than 3 sensors. In this example, you use four sensors to generate bistatic detections using one emitter.
Next, you will add a target to the scene to generate bistatic detections.
Add one target to scenario
Platforms without any attached emitters or sensors are referred to as targets. Create targets for tracking using platform.
% Add one target here using the platform method of scenario. Specify the % trajectory using a kinematicTrajectory with random position and constant % velocity. platform(scene,'Trajectory',kinematicTrajectory(... 'Position', [2000*randn 100*randn -1000],... 'Velocity',[10*randn 10*randn 5*randn])); % Initialize the display for visualization. theaterDisplay = helperBistaticRangeFusionDisplay(scene,... 'XLim',[-3 3],'YLim', [-3 3],'ZLim',[-2.5 0],... 'GIF',''); % records new GIF if name specified view(3);
In a scenario with a single target and no false alarms, multiple measurements can be triangulated to obtain the localized target position. This localized position can be used as an estimate of target position or can also be passed to a tracker to estimate the target state. Now, you will generate bistatic radar detections from a single target and visualize the geometry of bistatic ellipsoids. You will calculate the triangulated position using the supporting function helperBistaticRangeFusion, included with this example. The helperBistaticRangeFusion function calculates the triangulated position of the target, given the bistatic range detections generated by the target.
% Create a fused detection to represent the triangulated position and % visualize the position as a 3-D fused position detection. measParam = struct('Frame','Rectangular',... 'HasAzimuth',true,'HasElevation',true,... 'HasRange',true,'HasVelocity',false,... 'OriginPosition',[0;0;0],...% Fused position is in scenario frame 'OriginVelocity',[0;0;0],...% Scenario frame has zero velocity 'Orientation',eye(3),... % Scenario frame has no rotation. 'IsParentToChild',false); % Specify if rotation is specified in parent frame % Represent the fused detection using objectDetection. It has a 3-D % position and covariance. fusedDetection = {objectDetection(0,zeros(3,1),'MeasurementNoise',eye(3),... 'MeasurementParameters',measParam)}; % Change view view(-125,9); % Run scenario. while advance(scene) % Get current simulation time. time = scene.SimulationTime; % Get bistatic range detections from 1 target. detections = detectBistaticTargetRange(scene,time,emitterIdx,true); % Triangulate detections to estimate target position. [position, covariance] = helperBistaticRangeFusion(detections); % Update the fused detection. fusedDetection{1}.Measurement = position; fusedDetection{1}.MeasurementNoise = covariance; % Update the display. theaterDisplay([detections;fusedDetection]); end % Write new GIF if requested writeGIF(theaterDisplay);
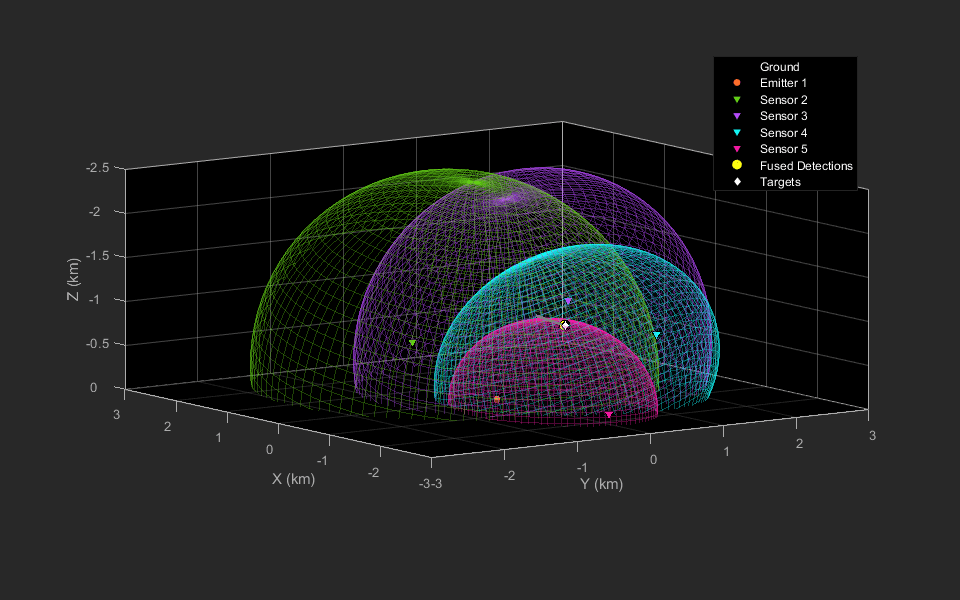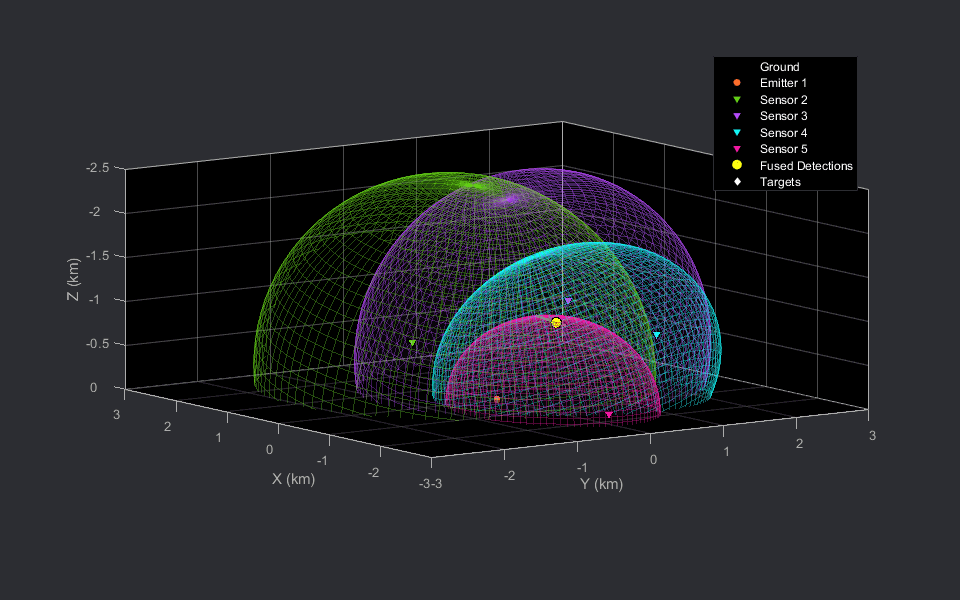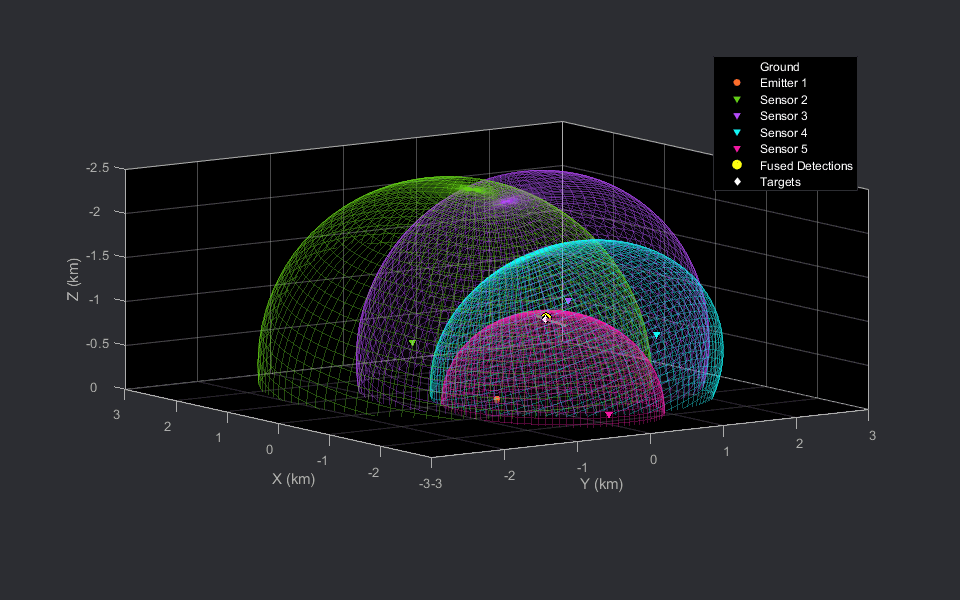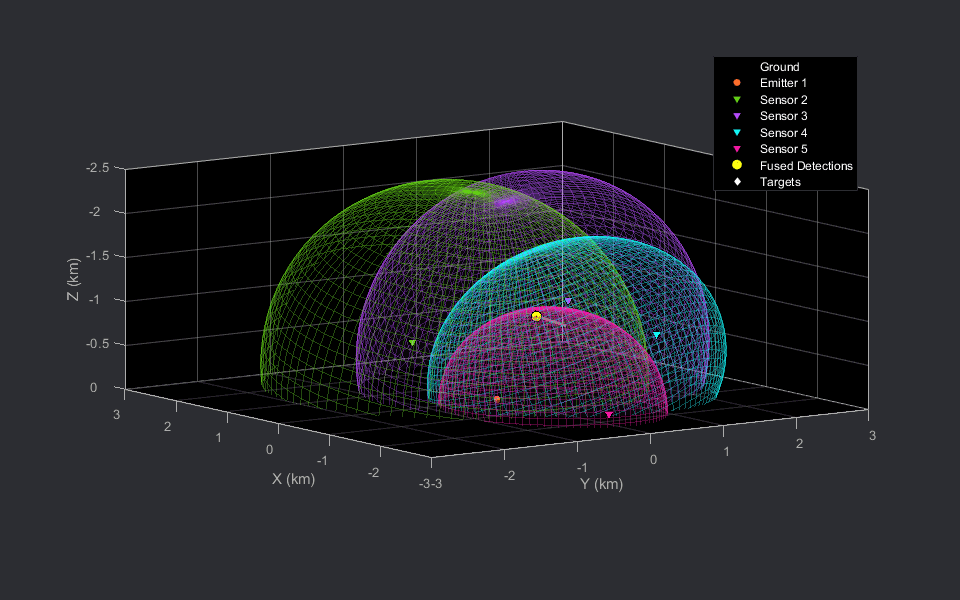
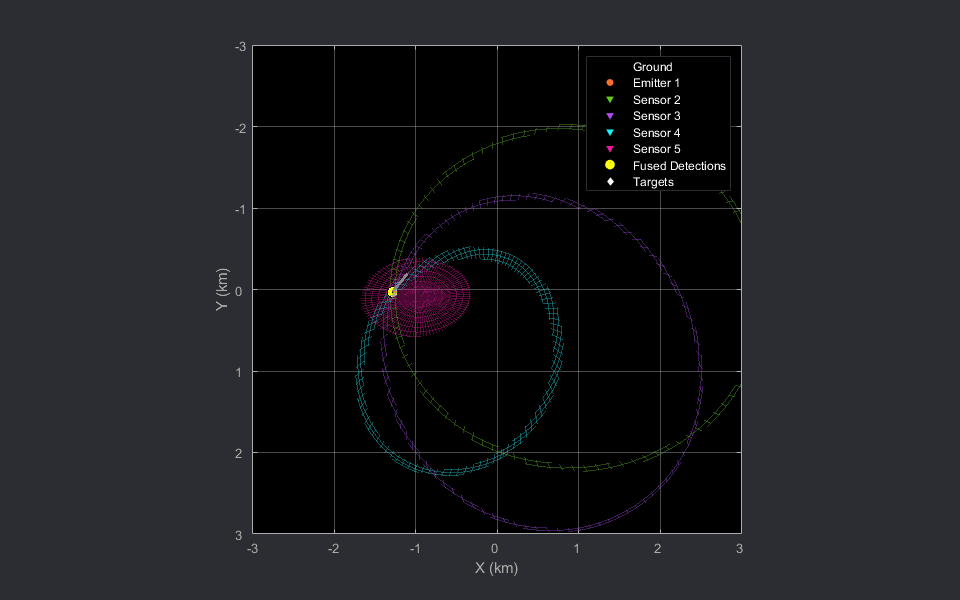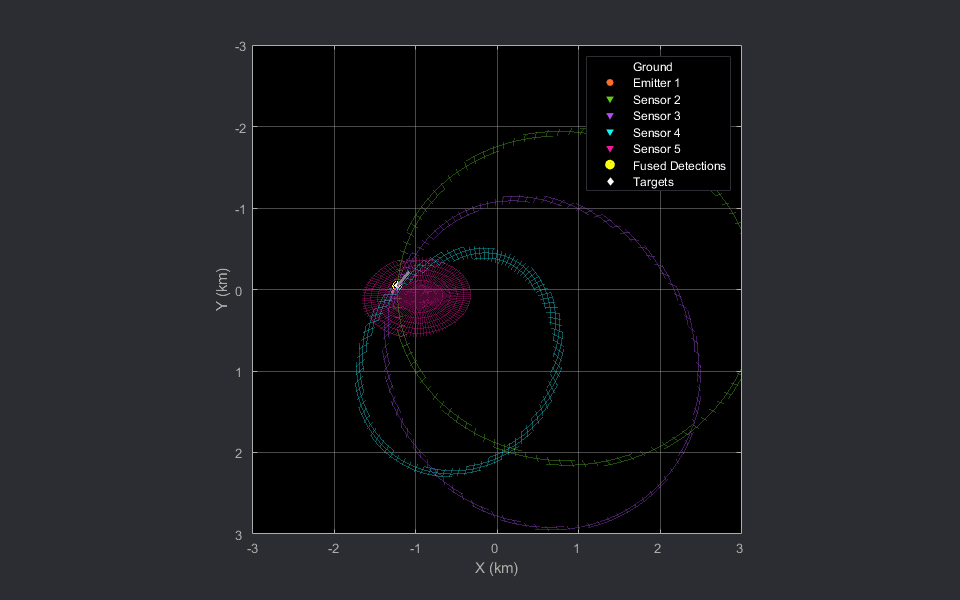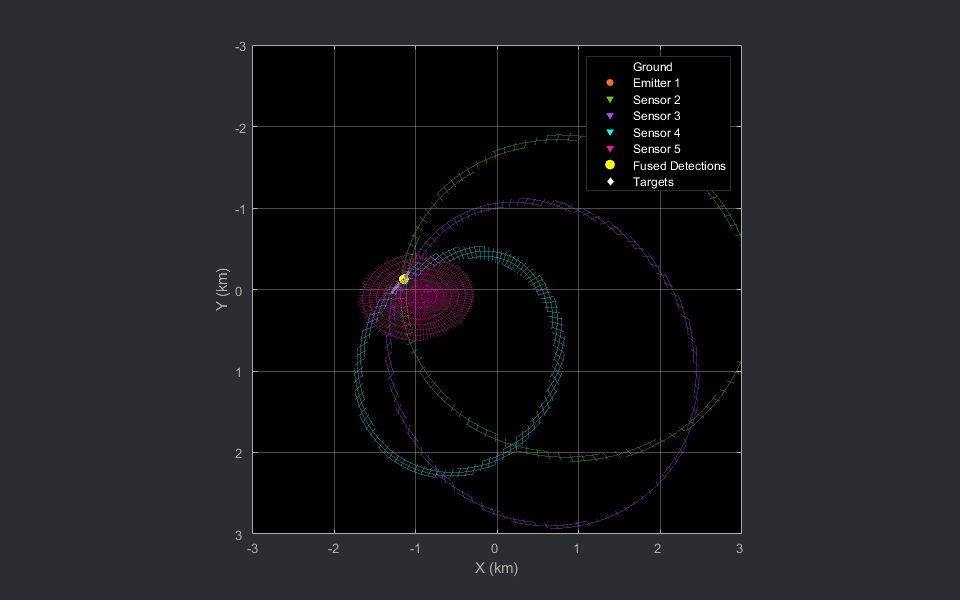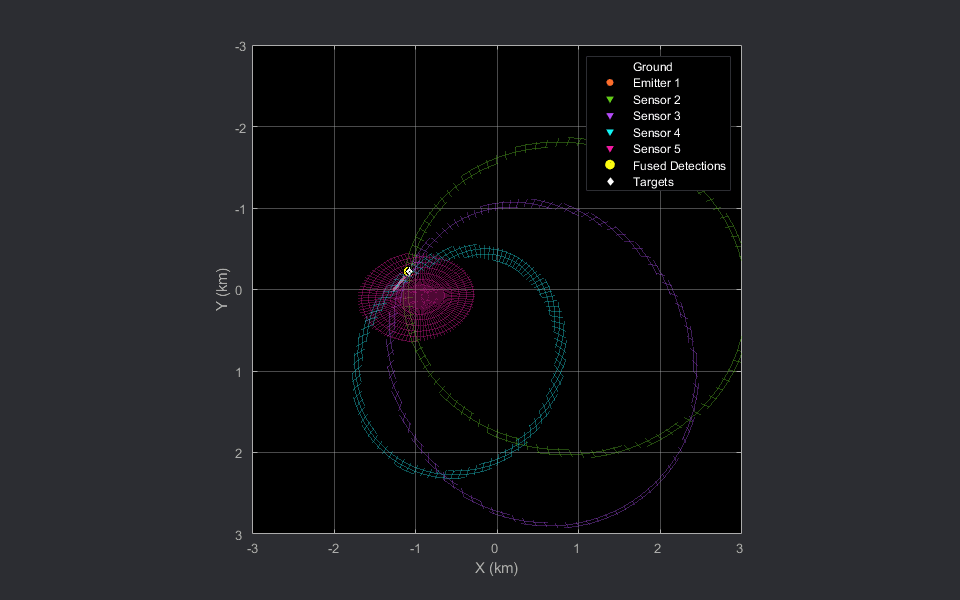
In the preceding animations, the bistatic radar sensors are depicted with the downward-pointing triangles. The stationary emitter is depicted with the purple circle marker at the origin. The target is denoted by the white diamond and the grey line shows the trajectory of the target. The 2-D animation is sliced at the target's Z location at each time stamp.
The fused detection, shown using the yellow circle marker, lies close to the intersection region generated the four ellipsoids and is close to the true position of the target during the scenario.
Multi-Target Scenario
The single-target scenario assumes that detections are known to be generated by the same target. Therefore, you can triangulate them to localize the target. However, in a multi-target scenario and in the presence of false alarms and missed detections, this information is usually not available. This results in the unknown data association between detections and the targets. To solve this problem, you use the staticDetectionFuser. The staticDetectionFuser estimates the unknown data association between detections and targets and finds the best solution using a multi-dimensional assignment formulation. The staticDetectionFuser outputs fused detections. The number of fused detections represent possible number of targets and each detection represents the Cartesian position of the target.
Next, you will add new targets to the scenario, and use the staticDetectionFuser to create fused detections from multiple targets in the presence of false alarms. These detections are further processed by a GNN tracker, trackerGNN, to track the targets.
% Restart the scenario and add remaining targets. restart(scene); % Reproducible geometry rng(2021); % Number of targets added here. numTargets = 4; % randomly distributed targets. r = abs(2000*randn(1,numTargets)); % Random ranges (m) theta = linspace(0,numTargets*pi/4,numTargets); % Angular position (rad) xTgt = r.*cos(theta) + 100*randn(1,numTargets); % x position (m) yTgt = -r.*sin(theta) + 100*randn(1,numTargets); % y position (m) % Targets above ground. zTgt = -1000*ones(1,numTargets); % z position (m) for iD = 1:numTargets thisPlat = platform(scene,... 'Trajectory',kinematicTrajectory('Position',[xTgt(iD) yTgt(iD) zTgt(iD)],... 'Velocity',[10*randn 10*randn 5*randn])); end % Update platforms variable. platforms = scene.Platforms; % Reset the display. release(theaterDisplay); % Turn off plotting for bistatic ellipse for all targets. theaterDisplay.PlotBistaticEllipse = false; % No recording theaterDisplay.GIF = ''; % Call once to plot new trajectories. theaterDisplay(); % Scenario display with trajectories. showScenario(theaterDisplay); snapnow; showGrabs(theaterDisplay,[]);
![]()
Setup Fuser and Tracker
This section creates a static detection fuser that uses the spherical intersection localization algorithm discussed earlier. Additionally, a Global Nearest Neighbor (GNN) tracker is defined to process the fused detections.
% Define a static detection fuser. fuser = staticDetectionFuser( ... 'MeasurementFusionFcn','helperBistaticRangeFusion', ... 'UseParallel',true, ... % Do parallel processing 'MaxNumSensors',numSensors, ... % Number of bistatic radar sensors 'Volume',sensor.RangeResolution, ... % Volumes of the sensors' detection bin 'MeasurementFormat','custom', ... % Define custom fused measurement as bistatic cannot not reported by cvmeas 'MeasurementFcn','helperBistaticMeas',... % Set measurement function for reporting bistatic measurement 'DetectionProbability',0.99 ... % Probability of detecting the target ); % Define a GNN tracker. tracker = trackerGNN('AssignmentThreshold',100);
Track Targets Using Static Fusion
The simulated bistatic detections are fused with the staticDetectionFuser using spherical intersection algorithm. The fused detections are then passed to the GNN tracker.
while advance(scene) % Get current simulation time. time = scene.SimulationTime; % Get bistatic range detections detections = detectBistaticTargetRange(scene,time,emitterIdx); % Fuse bistatic detections into one structure. [superDets, info] = fuser(detections); % Track fused bistatic detections using the GNN tracker. confTracks = tracker(superDets,scene.SimulationTime); % Update display with current platform positions and tracks. theaterDisplay([superDets(:);detections(:)],confTracks); end
Results
In the presence of multiple targets and possible false alarms, the ghost intersections may sometimes be more favorable than actual solution. As these ghost intersections appear randomly on the scenario, they are effectively treated as "false alarms" by the centralized tracker. You can notice in the figures below that the static fusion outputs detections at the incorrect positions. As ghost intersections compete with true intersections, two true targets are missed at this time.
In the "Current Estimated Tracks" plot, note that the tracker is able to maintain tracks on all 5 targets without creating any ghosts or false tracks.
showGrabs(theaterDisplay,1);
![]()
![]()
The plots below show the top view of tracks 1 and 2 with their histories at the end of the simulation. The history is represented by the orange line connecting the track. Notice that the track histories are close to the true trajectories of the targets.
showGrabs(theaterDisplay,2,false);
![]()
![]()
Summary
In this example, you learned how to simulate a scenario with bistatic sensors. You learned about the challenges associated with tracking targets using bistatic measurements. You used the staticDetectionFuser to fuse bistatic range detections from multiple targets and trackerGNN to track targets with the fused position measurements.
Supporting functions
helperBistaticRangeFusion Fuse range-only detections to triangulate target position
function [pos,cov] = helperBistaticRangeFusion(detections) % This function is for example purposes only and may be removed in a future % release. % This function returns the estimated position and covariance of the target % given the bistatic detections generated from it. % Copyright 2019 The MathWorks, Inc. % Do a coarse gating, as a minimum of 3 measurements are required for % finding a solution. if numel(detections) < 3 pos = 1e10*ones(3,1); cov = 2*eye(3); else % Retrieve info from measurements ranges = zeros(numel(detections),1); receiverLocations = zeros(3,numel(detections)); emitterLocation = detections{1}.MeasurementParameters.EmitterPosition; for i = 1:numel(detections) rLoc = detections{i}.MeasurementParameters(2).OriginPosition; receiverLocations(:,i) = rLoc; % The spherical intersection method assumes that measurment is % Remit + Rrecv. Bistatic measurement is defined as Remit + Rrecv - Rb. % Add the Rb to the actual measurement L = norm(emitterLocation(:) - rLoc(:)); ranges(i) = detections{i}.Measurement + L; end pos = helperSphericalIntersection(ranges,receiverLocations,emitterLocation); % Covariance is calculated only when required. This helps saving % computation during cost calculation for static fusion, where only % position is required. if nargout > 1 cov = linearFusionFcn(pos,detections); end end end %% linear fusion function for measurement noise function measCov = linearFusionFcn(pos,thisDetections) % Linear noise fusion function. It requires measJacobian to use linear % transformation. % Use a constant velocity state to calculate jacobians. estState = zeros(6,1); estState(1:2:end) = pos; n = numel(thisDetections); totalJacobian = zeros(n,3); totalCovariance = zeros(n,n); for i = 1:numel(thisDetections) H = cvmeasjac(estState,thisDetections{i}.MeasurementParameters); totalJacobian(i,:) = H(1,1:2:end); totalCovariance(i,i) = thisDetections{i}.MeasurementNoise; end toInvertJacobian = totalJacobian'/(totalCovariance)*totalJacobian; I = eye(3); % 2-D to 3-D conversion with 0 jacobian wrt z. if toInvertJacobian(3,3) == 0 toInvertJacobian(3,3) = 1; end measCov = I/toInvertJacobian; % Return true positive definite. measCov = (measCov + measCov')/2; measCov(~isfinite(measCov)) = 1000; % Some big number for inf and nan end
detectionBistaticTargetRange Generate bistatic range-only detections from targets in scenario.
function detections = detectBistaticTargetRange(scene,time,emitterIdx,removeFalseAlarms) % Get platforms from scenario. platforms = scene.Platforms; % A flag to indicate if false alarms should be removed from detections. if nargin == 3 removeFalseAlarms = false; end % Distinguish between receivers and targets to remove detections from % the receiver. It is assumed that these detections can be removed from % the batch using prior information. isReceiver = cellfun(@(x)~isempty(x.Sensors),scene.Platforms); allIDs = cellfun(@(x)x.PlatformID,scene.Platforms); receiverIDs = allIDs(isReceiver); % Generate RF emissions emitPlatform = platforms{emitterIdx}; txEmiss = emit(emitPlatform, time); % Propagate the emissions and reflect these emissions from platforms. reflSigs = radarChannel(txEmiss, platforms,'HasOcclusion',false); % Generate detections from the bistatic radar sensor. detections = {}; numPlat = numel(platforms); for iPlat = 1:numPlat thisPlatform = platforms{iPlat}; % Receive the emissions, calculate interference losses, and % generate bistatic detections. thisDet = detect(thisPlatform, reflSigs, time); % Remove the detections that are the bistatic receivers. Only the % detections from the target platforms will be fused and tracked. detectedTargetIDs = cellfun(@(x)x.ObjectAttributes{1}.TargetIndex,thisDet); toRemove = ismember(detectedTargetIDs, receiverIDs) | removeFalseAlarms*(detectedTargetIDs<=0); thisDet = thisDet(~toRemove); % Add this platform's detections to the detections array. detections = [detections; thisDet]; %#ok<AGROW> end % Determine emitter position and velocity for this simulation time. emitterPosition = emitPlatform.Trajectory.Position(:); % Update detections structure to indicate that only bistatic range measurements are retained. for iD = 1:numel(detections) detections{iD}.Measurement = detections{iD}.Measurement(end); %#ok<AGROW> % Range measurement detections{iD}.MeasurementNoise = detections{iD}.MeasurementNoise(end,end); %#ok<AGROW> % Measurement noise for range detections{iD}.MeasurementParameters(1).HasAzimuth = false; %#ok<AGROW> % Update measurement parameters to indicate that azimuth no longer exists detections{iD}.MeasurementParameters(1).HasElevation = false; %#ok<AGROW> % Update measurement parameters to indicate that elevation no longer exists detections{iD}.MeasurementParameters(1).EmitterPosition = emitterPosition; %#ok<AGROW> % Add emitter position end end
References
Malanowski, M. and K. Kulpa. "Two Methods for Target Localization in Multistatic Passive Radar." IEEE Transactions on Aerospace and Electronic Systems, Vol. 48, No. 1, Jan. 2012, pp. 572-578.
Willis, N. J. Bistatic Radar. Raleigh:SciTech Publishing, Inc., 2005.
