Introduction to Simulating IMU Measurements
This example shows how to simulate inertial measurement unit (IMU) measurements using the imuSensor System object. An IMU can include a combination of individual sensors, including a gyroscope, an accelerometer, and a magnetometer. You can specify properties of the individual sensors using gyroparams, accelparams, and magparams, respectively.
In the following plots, unless otherwise noted, only the x-axis measurements are shown. Use the sliders to interactively tune the parameters.
Default Parameters
The default parameters for the gyroscope model simulate an ideal signal. Given a sinusoidal input, the gyroscope output should match exactly.
params = gyroparams
params =
gyroparams with properties:
MeasurementRange: Inf rad/s
Resolution: 0 (rad/s)/LSB
ConstantBias: [0 0 0] rad/s
AxesMisalignment: [3⨯3 double] %
NoiseDensity: [0 0 0] (rad/s)/√Hz
BiasInstability: [0 0 0] rad/s
RandomWalk: [0 0 0] (rad/s)*√Hz
NoiseType: "double-sided"
BiasInstabilityCoefficients: [1⨯1 struct]
TemperatureBias: [0 0 0] (rad/s)/°C
TemperatureScaleFactor: [0 0 0] %/°C
AccelerationBias: [0 0 0] (rad/s)/(m/s²)
% Generate N samples at a sampling rate of Fs with a sinusoidal frequency % of Fc. N = 1000; Fs = 100; Fc = 0.25; t = (0:(1/Fs):((N-1)/Fs)).'; acc = zeros(N, 3); angvel = zeros(N, 3); angvel(:,1) = sin(2*pi*Fc*t); imu = imuSensor('SampleRate', Fs, 'Gyroscope', params); [~, gyroData] = imu(acc, angvel); figure plot(t, angvel(:,1), '--', t, gyroData(:,1)) xlabel('Time (s)') ylabel('Angular Velocity (rad/s)') title('Ideal Gyroscope Data') legend('x (ground truth)', 'x (gyroscope)')

Hardware Parameter Tuning
The following parameters model hardware limitations or defects. Some can be corrected through calibration.
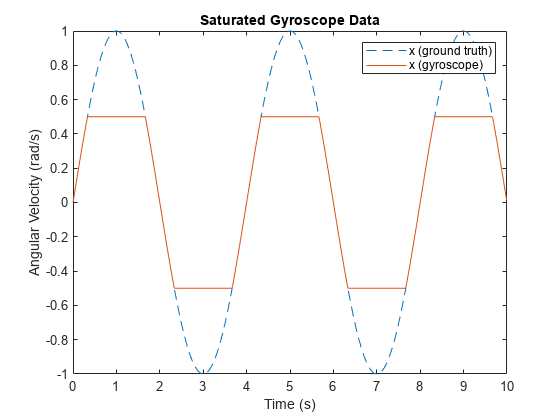
MeasurementRange determines the maximum absolute value reported by the gyroscope. Larger absolute values are saturated. The effect is shown by setting the measurement range to a value smaller than the amplitude of the sinusoidal ground-truth angular velocity.
imu = imuSensor('SampleRate', Fs, 'Gyroscope', params); imu.Gyroscope.MeasurementRange =0.5; % rad/s [~, gyroData] = imu(acc, angvel); figure plot(t, angvel(:,1), '--', t, gyroData(:,1)) xlabel('Time (s)') ylabel('Angular Velocity (rad/s)') title('Saturated Gyroscope Data') legend('x (ground truth)', 'x (gyroscope)')
Resolution affects the step size of the digital measurements. Use this parameter to model the quantization effects from the analog-to-digital converter (ADC). The effect is shown by increasing the parameter to a much larger value than is typical.
imu = imuSensor('SampleRate', Fs, 'Gyroscope', params); imu.Gyroscope.Resolution =0.5; % (rad/s)/LSB [~, gyroData] = imu(acc, angvel); figure plot(t, angvel(:,1), '--', t, gyroData(:,1)) xlabel('Time (s)') ylabel('Angular Velocity (rad/s)') title('Quantized Gyroscope Data') legend('x (ground truth)', 'x (gyroscope)')

AxesMisalignment is the amount of skew in the sensor axes. This skew normally occurs when the sensor is mounted to the PCB and can be corrected through calibration. The effect is shown by skewing the x-axis slightly and plotting both the x-axis and y-axis.
imu = imuSensor('SampleRate', Fs, 'Gyroscope', params); xMisalignment =2; % percent imu.Gyroscope.AxesMisalignment = [xMisalignment, 0, 0]; % percent [~, gyroData] = imu(acc, angvel); figure plot(t, angvel(:,1:2), '--', t, gyroData(:,1:2)) xlabel('Time (s)') ylabel('Angular Velocity (rad/s)') title('Misaligned Gyroscope Data') legend('x (ground truth)', 'y (ground truth)', ... 'x (gyroscope)', 'y (gyroscope)')

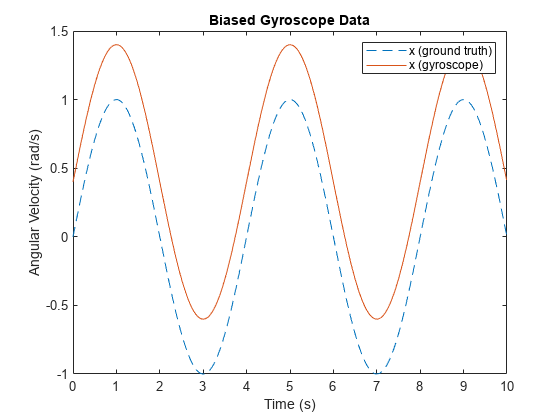
ConstantBias occurs in sensor measurements due to hardware defects. Since this bias is not caused by environmental factors, such as temperature, it can be corrected through calibration.
imu = imuSensor('SampleRate', Fs, 'Gyroscope', params); xBias =0.4; % rad/s imu.Gyroscope.ConstantBias = [xBias, 0, 0]; % rad/s [~, gyroData] = imu(acc, angvel); figure plot(t, angvel(:,1), '--', t, gyroData(:,1)) xlabel('Time (s)') ylabel('Angular Velocity (rad/s)') title('Biased Gyroscope Data') legend('x (ground truth)', 'x (gyroscope)')
Random Noise Parameter Tuning
The following parameters model random noise in sensor measurements. More information on these parameters can be found in the Inertial Sensor Noise Analysis Using Allan Variance example.
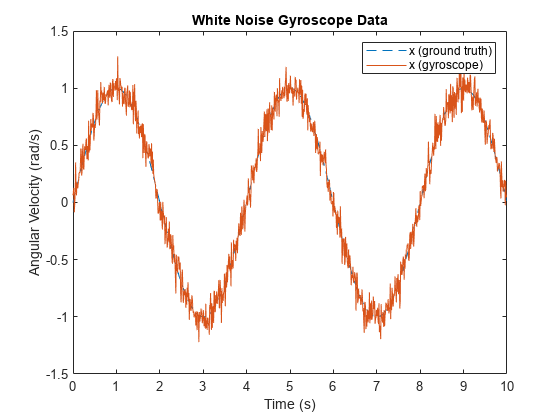
NoiseDensity is the amount of white noise in the sensor measurement. It is sometimes called angle random walk for gyroscopes or velocity random walk for accelerometers.
rng('default') imu = imuSensor('SampleRate', Fs, 'Gyroscope', params); imu.Gyroscope.NoiseDensity =0.0125; % (rad/s)/sqrt(Hz) [~, gyroData] = imu(acc, angvel); figure plot(t, angvel(:,1), '--', t, gyroData(:,1)) xlabel('Time (s)') ylabel('Angular Velocity (rad/s)') title('White Noise Gyroscope Data') legend('x (ground truth)', 'x (gyroscope)')
BiasInstability is the amount of pink or flicker noise in the sensor measurement.
imu = imuSensor('SampleRate', Fs, 'Gyroscope', params); imu.Gyroscope.BiasInstability =0.02; % rad/s [~, gyroData] = imu(acc, angvel); figure plot(t, angvel(:,1), '--', t, gyroData(:,1)) xlabel('Time (s)') ylabel('Angular Velocity (rad/s)') title('Bias Instability Gyroscope Data') legend('x (ground truth)', 'x (gyroscope)')

RandomWalk is the amount of Brownian noise in the sensor measurement. It is sometimes called rate random walk for gyroscopes or acceleration random walk for accelerometers.
imu = imuSensor('SampleRate', Fs, 'Gyroscope', params); imu.Gyroscope.RandomWalk =0.091; % (rad/s)*sqrt(Hz) [~, gyroData] = imu(acc, angvel); figure plot(t, angvel(:,1), '--', t, gyroData(:,1)) xlabel('Time (s)') ylabel('Angular Velocity (rad/s)') title('Random Walk Gyroscope Data') legend('x (ground truth)', 'x (gyroscope)')

Environmental Parameter Tuning
The following parameters model noise that arises from changes to the environment of the sensor.
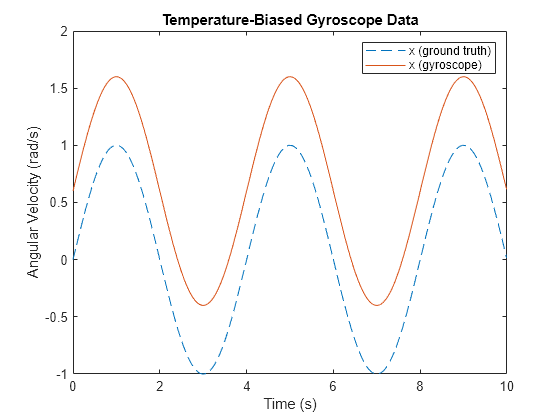
TemperatureBias is the bias added to sensor measurements due to temperature difference from the default operating temperature. Most sensor datasheets list the default operating temperature as 25 degrees Celsius. This bias is shown by setting the parameter to a non-zero value and setting the operating temperature to a value above 25 degrees Celsius.
imu = imuSensor('SampleRate', Fs, 'Gyroscope', params); imu.Gyroscope.TemperatureBias =0.06; % (rad/s)/(degrees C) imu.Temperature = 35; [~, gyroData] = imu(acc, angvel); figure plot(t, angvel(:,1), '--', t, gyroData(:,1)) xlabel('Time (s)') ylabel('Angular Velocity (rad/s)') title('Temperature-Biased Gyroscope Data') legend('x (ground truth)', 'x (gyroscope)')
TemperatureScaleFactor is the error in the sensor scale factor due to changes in the operating temperature. This causes errors in the scaling of the measurement; in other words smaller ideal values have less error than larger values. This error is shown by linearly increasing the temperature.
imu = imuSensor('SampleRate', Fs, 'Gyroscope', params); imu.Gyroscope.TemperatureScaleFactor =3.2; % %/(degrees C) standardTemperature = 25; % degrees C temperatureSlope = 2; % (degrees C)/s temperature = temperatureSlope*t + standardTemperature; gyroData = zeros(N, 3); for i = 1:N imu.Temperature = temperature(i); [~, gyroData(i,:)] = imu(acc(i,:), angvel(i,:)); end figure plot(t, angvel(:,1), '--', t, gyroData(:,1)) xlabel('Time (s)') ylabel('Angular Velocity (rad/s)') title('Temperature-Scaled Gyroscope Data') legend('x (ground truth)', 'x (gyroscope)')

AccelerationBias is the bias added to the gyroscope measurement due to linear accelerations. This parameter is specific to the gyroscope. This bias is shown by setting the parameter to a non-zero value and using a non-zero input acceleration.
imu = imuSensor('SampleRate', Fs, 'Gyroscope', params); imu.Gyroscope.AccelerationBias =0.3; % (rad/s)/(m/s^2) acc(:,1) = 1; [~, gyroData] = imu(acc, angvel); figure plot(t, angvel(:,1), '--', t, gyroData(:,1)) xlabel('Time (s)') ylabel('Angular Velocity (rad/s)') title('Acceleration-Biased Gyroscope Data') legend('x (ground truth)', 'x (gyroscope)')

