The Multiplication Process
The multiplication of an n-bit binary number with an m-bit binary number results in a product that is up to m + n bits in length for both signed and unsigned words.
Suppose you want to multiply three numbers. Each of these numbers is represented by a 5-bit word, and each has a different binary-point-only scaling. Additionally, the output is restricted to a 10-bit word with binary-point-only scaling of 2-4. The multiplication is shown in the following model for the input values 5.75, 2.375, and 1.8125.
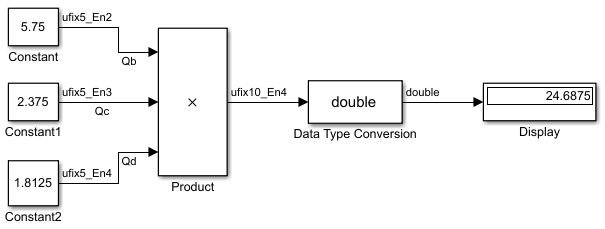
Applying the rules from the previous section, the multiplication follows these steps:
The first two numbers (5.75 and 2.375) are multiplied:
Note that the binary point of the product is given by the sum of the binary points of the multiplied numbers.
The result of step 1 is converted to the output data type:
Signal Conversions discusses conversions. Note that a loss in precision of one bit occurs, with the resulting value of QTemp determined by the rounding mode. For this example, round-to-floor is used. Furthermore, overflow did not occur but is possible for this operation.
The result of step 2 and the third number (1.8125) are multiplied:
Note that the binary point of the product is given by the sum of the binary points of the multiplied numbers.
The product is converted to the output data type:
Signal Conversions discusses conversions. Note that a loss in precision of 4 bits occurred, with the resulting value of QTemp determined by the rounding mode. For this example, round-to-floor is used. Furthermore, overflow did not occur but is possible for this operation.
Blocks that perform multiplication include the Product, Discrete FIR Filter, and Gain blocks.