The Division Process
The C programming language provides access to integer division only for fixed-point data types. Depending on the size of the numerator, you can obtain some of the fractional bits by performing a shift prior to the integer division.
Suppose you want to divide two numbers. Each of these numbers is represented by an 8-bit word, and each has a binary-point-only scaling of 2-4. Additionally, the output is restricted to an 8-bit word with binary-point-only scaling of 2-4.
The division of 9.1875 by 1.5000 is shown in the following model.
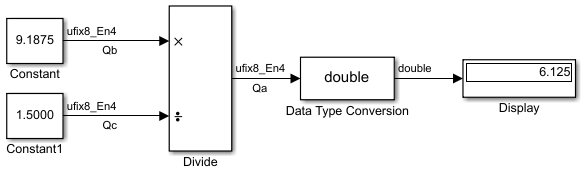
For this example,
Assuming a large data type was available, this could be implemented as
where the numerator uses the larger data type. If a larger data type was not available, integer division combined with four repeated subtractions would be used. Both approaches produce the same result, with the former being more efficient.