Propose Data Types Based on Simulation Ranges Using the fiaccel
Function
This example shows how to propose fixed-point
data types based on simulation range data using the fiaccel function.
Prerequisites
To complete this example, you must install the following products:
MATLAB®
Fixed-Point Designer™
C compiler
See Supported Compilers.
You can use
mex -setupto change the default compiler. See Change Default Compiler.
Create a New Folder and Copy Relevant Files
In a local, writable folder, create a function
ex_2ndOrder_filter.m.function y = ex_2ndOrder_filter(x) %#codegen persistent z if isempty(z) z = zeros(2,1); end % [b,a] = butter(2, 0.25) b = [0.0976310729378175, 0.195262145875635, 0.0976310729378175]; a = [1, -0.942809041582063, 0.3333333333333333]; y = zeros(size(x)); for i = 1:length(x) y(i) = b(1)*x(i) + z(1); z(1) = b(2)*x(i) + z(2) - a(2) * y(i); z(2) = b(3)*x(i) - a(3) * y(i); end end
Create a test file,
ex_2ndOrder_filter_test.m, to exercise theex_2ndOrder_filteralgorithm.It is best practice to create a separate test script to do all the pre- and post-processing such as loading inputs, setting up input values, calling the function under test, and outputting test results.
To cover the full intended operating range of the system, the test script runs the
ex_2ndOrder_filterfunction with three input signals: chirp, step, and impulse. The script then plots the outputs.% ex_2ndOrder_filter_test % % Define representative inputs N = 256; % Number of points t = linspace(0,1,N); % Time vector from 0 to 1 second f1 = N/2; % Target frequency of chirp set to Nyquist x_chirp = sin(pi*f1*t.^2); % Linear chirp from 0 to Fs/2 Hz in 1 second x_step = ones(1,N); % Step x_impulse = zeros(1,N); % Impulse x_impulse(1) = 1; % Run the function under test x = [x_chirp;x_step;x_impulse]; y = zeros(size(x)); for i = 1:size(x,1) y(i,:) = ex_2ndOrder_filter(x(i,:)); end % Plot the results titles = {'Chirp','Step','Impulse'} clf for i = 1:size(x,1) subplot(size(x,1),1,i) plot(t,x(i,:),t,y(i,:)) title(titles{i}) legend('Input','Output') end xlabel('Time (s)') figure(gcf) disp('Test complete.')
| Type | Name | Description |
|---|---|---|
| Function code | ex_2ndOrder_filter.m | Entry-point MATLAB function |
| Test file | ex_2ndOrder_filter_test.m | MATLAB script that tests
ex_2ndOrder_filter.m |
Set Up the Fixed-Point Configuration Object
Create a fixed-point configuration object and configure the test file name.
cfg = coder.config('fixpt'); cfg.TestBenchName = 'ex_2ndOrder_filter_test';
Collect Simulation Ranges and Generate Fixed-Point Code
Use the fiaccel function to convert the floating-point MATLAB function, ex_2ndOrder_filter,
to fixed-point MATLAB code. Set the default
word length for the fixed-point data types to 16.
cfg.ComputeSimulationRanges = true; cfg.DefaultWordLength = 16; % Derive ranges and generate fixed-point code fiaccel -float2fixed cfg ex_2ndOrder_filter
fiaccel analyzes the floating-point
code. Because you did not specify the input types for the ex_2ndOrder_filter function,
the conversion process infers types by simulating the test file. The
conversion process then derives ranges for variables in the algorithm.
It uses these derived ranges to propose fixed-point types for these
variables. When the conversion is complete, it generates a type proposal
report.
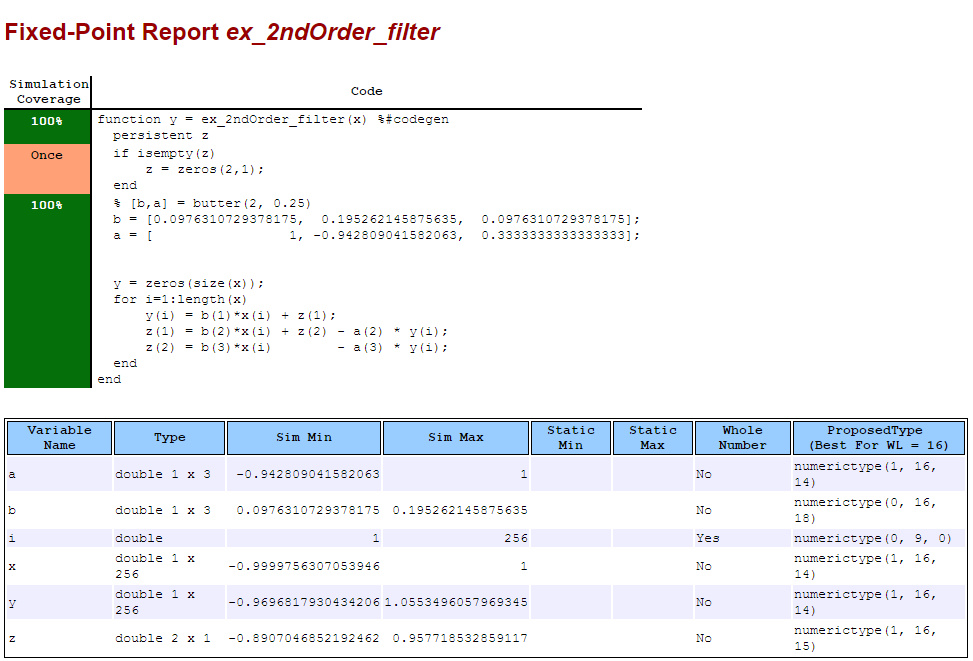
View Range Information
Click the link to the type proposal report for the ex_2ndOrder_filter function, ex_2ndOrder_filter_report.html.
The report opens in a web browser.
View Generated Fixed-Point MATLAB Code
fiaccel generates a fixed-point version
of the ex_2ndOrder_filter.m function, ex_2ndOrder_filter_fixpt.m,
and a wrapper function that calls ex_2ndOrder_filter_fixpt.
These files are generated in the codegen\ex_2ndOrder_filter\fixpt folder
in your local working folder.
function y = ex_2ndOrder_filter_fixpt(x) %#codegen fm = get_fimath(); persistent z if isempty(z) z = fi(zeros(2,1),1,16,15,fm); end % [b,a] = butter(2, 0.25) b = fi([0.0976310729378175,0.195262145875635,0.0976310729378175],... 0,16,18,fm); a = fi([1,-0.942809041582063,0.3333333333333333],1,16,14,fm); y = fi(zeros(size(x)),1,16,14,fm); for i=1:length(x) y(i) = b(1)*x(i) + z(1); z(1) = fi_signed(b(2)*x(i) + z(2)) - a(2) * y(i); z(2) = fi_signed(b(3)*x(i)) - a(3) * y(i); end end function y = fi_signed(a) coder.inline('always'); if isfi(a) && ~(issigned(a)) nt = numerictype(a); new_nt = numerictype(1,nt.WordLength + 1,... nt.FractionLength); y = fi(a,new_nt,fimath(a)); else y = a; end end function fm = get_fimath() fm = fimath('RoundingMethod','Floor',... 'OverflowAction','Wrap',... 'ProductMode','FullPrecision',... 'MaxProductWordLength',128,... 'SumMode','FullPrecision',... 'MaxSumWordLength',128); end