Propose Data Types Based on Derived Ranges Using the fiaccel Function

This example shows how to propose fixed-point data types based on static ranges using the fiaccel function. The advantage of proposing data types based on derived ranges is that you do not have to provide test files that exercise your algorithm over its full operating range. Running such test files often takes a very long time so you can save time by deriving ranges instead.

Note

Derived range analysis is not supported for non-scalar variables.

Prerequisites

To complete this example, you must install the following products:

Create a New Folder and Copy Relevant Files

  1. In a local, writable folder, create a function dti.m.

    The dti function implements a Discrete Time Integrator in MATLAB.

    function [y, clip_status] = dti(u_in) %#codegen
% Discrete Time Integrator in MATLAB
%  
% Forward Euler method, also known as Forward 
% Rectangular, or left-hand approximation. 
% The resulting expression for the output of 
% the block at step 'n' is 
% y(n) = y(n-1) + K * u(n-1)
%

init_val = 1;  
gain_val = 1;
limit_upper = 500;
limit_lower = -500;

% Variable to hold state between 
% consecutive calls to this block
persistent u_state;
if isempty(u_state)
    u_state = init_val+1;
end 

% Compute Output
if (u_state > limit_upper)
    y = limit_upper;
    clip_status = -2;
elseif (u_state >= limit_upper)
    y = limit_upper;
    clip_status = -1;
elseif (u_state < limit_lower)
	y = limit_lower;
    clip_status = 2;
elseif (u_state <= limit_lower)
	y = limit_lower;
    clip_status = 1;   
else        
    y = u_state;
    clip_status = 0;
end

% Update State
tprod = gain_val * u_in;
u_state = y + tprod;

  2. Create a test file, dti_test.m, to exercise the dti algorithm.

    The test script runs the dti function with a sine wave input. The script then plots the input and output signals.

    % dti_test
% cleanup
clear dti

% input signal
x_in = sin(2.*pi.*(0:0.001:2)).';

pause(10);

len = length(x_in);
y_out = zeros(1,len);
is_clipped_out = zeros(1,len);

for ii=1:len
    data = x_in(ii);
    % call to the dti function
    init_val = 0;
    gain_val = 1;
    upper_limit = 500;
    lower_limit = -500;
    
    % call to the design that does DTI
    [y_out(ii), is_clipped_out(ii)] = dti(data);
    
end

figure('Name', [mfilename, '_plot']);
subplot(2,1,1)
plot(1:len,x_in)
xlabel('Time')
ylabel('Amplitude')
title('Input Signal (Sin)')

subplot(2,1,2)
plot(1:len,y_out)
xlabel('Time')
ylabel('Amplitude')
title('Output Signal (DTI)')

disp('Test complete.');

It is a best practice is to create a separate test script to do pre- and post-processing, such as:

  • Loading inputs.

  • Setting up input values.

  • Outputting test results.

TypeNameDescription
Function codedti.mEntry-point MATLAB function
Test filedti_test.mMATLAB script that tests dti.m

Set Up the Fixed-Point Configuration Object

Create a fixed-point configuration object and configure the test file name.

fixptcfg = coder.config('fixpt');
fixptcfg.TestBenchName = 'dti_test';

Specify Design Ranges

Specify design range information for the dti function input parameter u_in. 

fixptcfg.addDesignRangeSpecification('dti', 'u_in', -1.0, 1.0)

Enable Plotting Using the Simulation Data Inspector

Select to run the test file to verify the generated fixed-point MATLAB code. Log inputs and outputs for comparison plotting and select to use the Simulation Data Inspector to plot the results.

fixptcfg.TestNumerics = true;
fixptcfg.LogIOForComparisonPlotting = true;
fixptcfg.PlotWithSimulationDataInspector = true;

Derive Ranges and Generate Fixed-Point Code

Use the fiaccel function to convert the floating-point MATLAB function, dti, to fixed-point MATLAB code. Set the default word length for the fixed-point data types to 16.

fixptcfg.ComputeDerivedRanges = true;
fixptcfg.ComputeSimulationRanges = false;
fixptcfg.DefaultWordLength = 16;

% Derive ranges  and generate fixed-point code
fiaccel -float2fixed fixptcfg dti

fiaccel analyzes the floating-point code. Because you did not specify the input types for the dti function, the conversion process infers types by simulating the test file. The conversion process then derives ranges for variables in the algorithm. It uses these derived ranges to propose fixed-point types for these variables. When the conversion is complete, it generates a type proposal report.

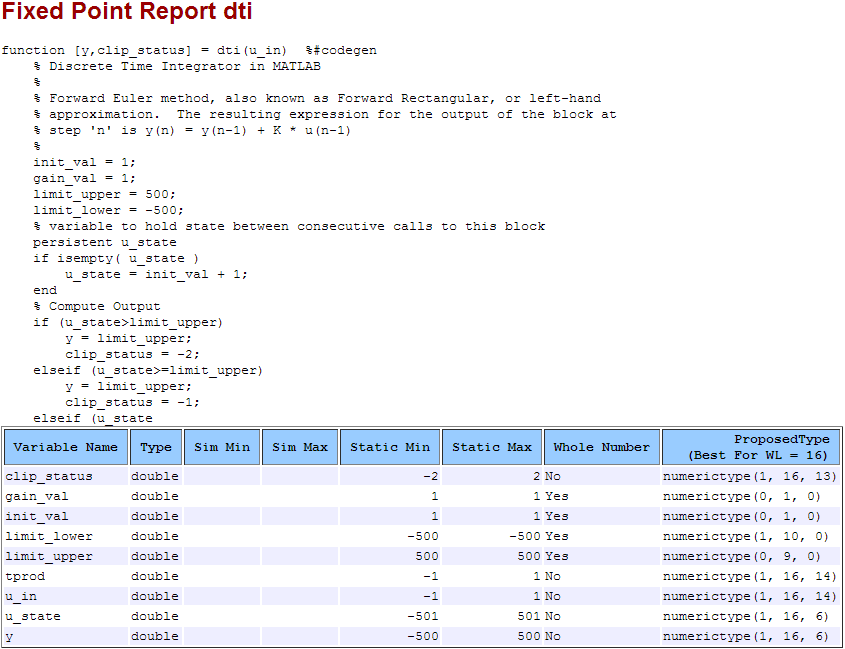
View Derived Range Information

Click the link to the type proposal report for the dti function, dti_report.html.

The report opens in a web browser.

View Generated Fixed-Point MATLAB Code

fiaccel generates a fixed-point version of the dti function, dti_fxpt.m, and a wrapper function that calls dti_fxpt. These files are generated in the codegen\dti\fixpt folder in your local working folder.

function [y, clip_status] = dti_fixpt(u_in) %#codegen
% Discrete Time Integrator in MATLAB
%  
% Forward Euler method, also known as 
% Forward Rectangular, or left-hand approximation.
% The resulting expression for the output of the 
% block at step 'n' is y(n) = y(n-1) + K * u(n-1)
%
fm = get_fimath();

init_val = fi(1,0,1,0,fm);  
gain_val = fi(1,0,1,0,fm);
limit_upper = fi(500,0,9,0,fm);
limit_lower = fi(-500,1,10,0,fm);

% variable to hold state between 
% consecutive calls to this block
persistent u_state;
if isempty(u_state)
    u_state = fi(init_val+fi(1,0,1,0,fm),1,16,6,fm);
end 

% Compute Output
if (u_state > limit_upper)
    y = fi(limit_upper, 1, 16, 6, fm);
    clip_status = fi(-2, 1, 16, 13, fm);
elseif (u_state >= limit_upper)
    y = fi(limit_upper, 1, 16, 6, fm);
    clip_status = fi(-1, 1, 16, 13, fm);
elseif (u_state < limit_lower)
	y = fi(limit_lower, 1, 16, 6, fm);
    clip_status = fi(2, 1, 16, 13, fm);
elseif (u_state <= limit_lower)
	y = fi(limit_lower, 1, 16, 6, fm);
    clip_status = fi(1, 1, 16, 13, fm);   
else        
    y = fi(u_state, 1, 16, 6, fm);
    clip_status = fi(0, 1, 16, 13, fm);
end

% Update State
tprod = fi(gain_val * u_in, 1, 16, 14, fm);
u_state(:) = y + tprod;
end


function fm = get_fimath()
	fm = fimath('RoundingMethod','Floor',...
        'OverflowAction','Wrap',...
        'ProductMode','FullPrecision',...
        'MaxProductWordLength',128,...
        'SumMode','FullPrecision',...
        'MaxSumWordLength',128);
end

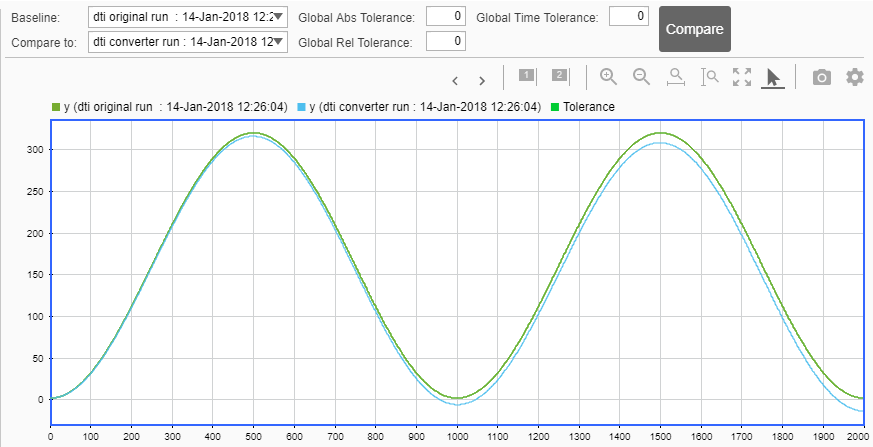
Compare Floating-Point and Fixed-Point Runs

Because you selected to log inputs and outputs for comparison plots and to use the Simulation Data Inspector for these plots, the Simulation Data Inspector opens.

You can use the Simulation Data Inspector to view floating-point and fixed-point run information and compare results. For example, to compare the floating-point and fixed-point values for the output y, on the Compare tab, select y, and then click Compare Runs.

The Simulation Data Inspector displays a plot of the baseline floating-point run against the fixed-point run and the difference between them.