Evaluate and Visualize Lane Boundary Detections Against Ground Truth
This example shows how to evaluate the performance of lane boundary detection against known ground truth. In this example, you will characterize the performance of a lane boundary detection algorithm on a per-frame basis by computing a goodness-of-fit measure. This measure can be used to pinpoint, visualize, and understand failure modes in the underlying algorithm.
Overview
With increasing interest in vision-based solutions to automated driving problems, being able to evaluate and verify the accuracy of detection algorithms has become very important. Verifying accuracy is especially important in detection algorithms that have several parameters that can be tuned to achieve results that satisfy predefined quality requirements. This example walks through one such workflow, where lane boundaries can be measured for their level of accuracy. This workflow helps pinpoint failure modes in these algorithms on a per-frame basis, as well as characterize its overall performance. This workflow also helps you visually and quantitatively understand the performance of the algorithm. You can then use this understanding to tune the underlying algorithm to improve its performance.
Load Ground Truth Data
The dataset used in this example is a video file from a front-mounted camera on a vehicle driving through a street. Ground truth for the lane boundaries has been manually marked on the video with the Ground Truth Labeler app, using a Line ROI labeled "LaneBoundary." This video is 8 seconds, or 250 frames long. It has three intersection crossings, several vehicles (parked and moving), and lane boundaries (double line, single, and dashed). To create a ground truth lane boundary dataset for your own video, you can use the Ground Truth Labeler app.
% Load MAT file with ground truth data. loaded = load('caltech_cordova1_laneAndVehicleGroundTruth.mat');
The loaded structure contains three fields:
groundTruthData, a timetable with two columns:LaneBoundariesandVehicles.LaneBoundariescontains ground truth points for the ego lane boundaries (left and right), represented as a cell array of XY points forming a poly line.Vehiclescontains ground truth bounding boxes for vehicles in the camera view, represented as M-by-4 arrays of [x,y,width,height].sensor, amonoCameraobject with properties about the calibrated camera mounted on the vehicle. This object lets you estimate the real-world distances between the vehicle and the objects in front of it.videoName, a character array containing the file name of the video where the frames are stored.
From the data in this structure, open the video file by using VideoReader to loop through the frames. The VideoReader object uses a helperMonoSensor object to detect lanes and objects in the video frame, using the camera setup stored in sensor. A timetable variable stored in gtdata holds the ground truth data. This variable contains the per-frame data that is used for analysis later on.
% Create a VideoReader object to read frames of the video. videoName = loaded.videoName; fileReader = VideoReader(videoName); % The ground truth data is organized in a timetable. gtdata = loaded.groundTruthData; % Display the first few rows of the ground truth data. head(gtdata)
Time Vehicles LaneBoundaries
____________ ____________ ______________
0 sec {6x4 double} {2x1 cell}
0.033333 sec {6x4 double} {2x1 cell}
0.066667 sec {6x4 double} {2x1 cell}
0.1 sec {6x4 double} {2x1 cell}
0.13333 sec {6x4 double} {2x1 cell}
0.16667 sec {6x4 double} {2x1 cell}
0.2 sec {6x4 double} {2x1 cell}
0.23333 sec {5x4 double} {2x1 cell}
The gtdata timetable has the columns Vehicles and LaneBoundaries. At each timestamp, the Vehicles column holds an M-by-4 array of vehicle bounding boxes and the LaneBoundaries column holds a two-element cell array of left and right lane boundary points.
First, visualize the loaded ground truth data for an image frame.
% Read the first frame of the video. frame = readFrame(fileReader); % Extract all lane points in the first frame. lanePoints = gtdata.LaneBoundaries{1}; % Extract vehicle bounding boxes in the first frame. vehicleBBox = gtdata.Vehicles{1}; % Superimpose the right lane points and vehicle bounding boxes. frame = insertMarker(frame, lanePoints{2}, 'X'); frame = insertObjectAnnotation(frame, 'rectangle', vehicleBBox, 'Vehicle'); % Display ground truth data on the first frame. figure imshow(frame)

Run Lane Boundary Detection Algorithm
Using the video frames and the monoCamera parameters, you can automatically estimate locations of lane boundaries. For illustration, the processFrame method of the helperMonoSensor class is used here to detect lane boundaries (as parabolicLaneBoundary objects) and vehicles (as [x, y, width, height] bounding box matrices). For the purpose of this example, this is the lane boundary detection "algorithm under test." You can use the same pattern for evaluating a custom lane boundary detection algorithm, where processFrame is replaced with the custom detection function. The ground truth points in the vehicle coordinates are also stored in the LanesInVehicleCoord column of the gtdata timetable. That way, they can be visualized in a Bird's-Eye View display later on. First, configure the helperMonoSensor object with the sensor. The helperMonoSensor class assembles all the necessary steps required to run the lane boundary detection algorithm.
% Set up monoSensorHelper to process video. monoCameraSensor = loaded.sensor; monoSensorHelper = helperMonoSensor(monoCameraSensor); % Create new timetable with same Time vector for measurements. measurements = timetable(gtdata.Time); % Set up timetable columns for holding lane boundary and vehicle data. numFrames = floor(fileReader.FrameRate*fileReader.Duration); measurements.LaneBoundaries = cell(numFrames, 2); measurements.VehicleDetections = cell(numFrames, 1); gtdata.LanesInVehicleCoord = cell(numFrames, 2); % Rewind the video to t = 0, and create a frame index to hold current % frame. fileReader.CurrentTime = 0; frameIndex = 0; % Loop through the videoFile until there are no new frames. while hasFrame(fileReader) frameIndex = frameIndex+1; frame = readFrame(fileReader); % Use the processFrame method to compute detections. % This method can be replaced with a custom lane detection method. detections = processFrame(monoSensorHelper, frame); % Store the estimated lane boundaries and vehicle detections. measurements.LaneBoundaries{frameIndex} = [detections.leftEgoBoundary ... detections.rightEgoBoundary]; measurements.VehicleDetections{frameIndex} = detections.vehicleBoxes; % To facilitate comparison, convert the ground truth lane points to the % vehicle coordinate system. gtPointsThisFrame = gtdata.LaneBoundaries{frameIndex}; vehiclePoints = cell(1, numel(gtPointsThisFrame)); for ii = 1:numel(gtPointsThisFrame) vehiclePoints{ii} = imageToVehicle(monoCameraSensor, gtPointsThisFrame{ii}); end % Store ground truth points expressed in vehicle coordinates. gtdata.LanesInVehicleCoord{frameIndex} = vehiclePoints; end
Now that you have processed the video with a lane detection algorithm, verify that the ground truth points are correctly transformed into the vehicle coordinate system. The first entry in the LanesInVehicleCoord column of the gtdata timetable contains the vehicle coordinates for the first frame. Plot these ground truth points on the first frame in the Bird's-Eye View.
% Rewind video to t = 0. fileReader.CurrentTime = 0; % Read the first frame of the video. frame = readFrame(fileReader); birdsEyeImage = transformImage(monoSensorHelper.BirdsEyeConfig, frame); % Extract right lane points for the first frame in Bird's-Eye View. firstFrameVehiclePoints = gtdata.LanesInVehicleCoord{1}; pointsInBEV = vehicleToImage(monoSensorHelper.BirdsEyeConfig, firstFrameVehiclePoints{2}); % Superimpose points on the frame. birdsEyeImage = insertMarker(birdsEyeImage, pointsInBEV, 'X', 'Size', 6); % Display transformed points in Bird's-Eye View. figure imshow(birdsEyeImage)

Measure Detection Errors
Computing the errors in lane boundary detection is an essential step in verifying the performance of several downstream subsystems. Such subsystems include lane departure warning systems that depend on the accuracy of the lane detection subsystem.
You can estimate this accuracy by measuring the goodness of fit. With the ground truth points and the estimates computed, you can now compare and visualize them to find out how well the detection algorithms perform.
The goodness of fit can be measured either at the per-frame level or for the entire video. The per-frame statistics provide detailed information about specific scenarios, such as the behavior at road bends where the detection algorithm performance may vary. The global statistics provide a big picture estimate of number of lanes that missed detection.
Use the evaluateLaneBoundaries function to return global detection statistics and an assignments array. This array matches the estimated lane boundary objects with corresponding ground truth points.
The threshold parameter in the evaluateLaneBoundaries function represents the maximum lateral distance in vehicle coordinates to qualify as a match with the estimated parabolic lane boundaries.
threshold = 0.25; % in meters [numMatches, numMisses, numFalsePositives, assignments] = ... evaluateLaneBoundaries(measurements.LaneBoundaries, ... gtdata.LanesInVehicleCoord, ... threshold); disp(['Number of matches: ', num2str(numMatches)]); disp(['Number of misses: ', num2str(numMisses)]); disp(['Number of false positives: ', num2str(numFalsePositives)]);
Number of matches: 402 Number of misses: 43 Number of false positives: 30
Using the assignments array, you can compute useful per-lane metrics, such as the average lateral distance between the estimates and the ground truth points. Such metrics indicate how well the algorithm is performing. To compute the average distance metric, use the helper function helperComputeLaneStatistics, which is defined at the end of this example.
averageDistance = helperComputeLaneStatistics(measurements.LaneBoundaries, ... gtdata.LanesInVehicleCoord, ... assignments, @mean); % Plot average distance between estimates and ground truth. figure stem(gtdata.Time, averageDistance) title('Average Distance Between Estimates and Ground Truth') grid on ylabel('Distance in Meters') legend('Left Boundary','Right Boundary')

Visualize and Review Differences Between Ground Truth and Your Algorithm
You now have a quantitative understanding of the accuracy of the lane detection algorithm. However, it is not possible to completely understand the failures solely based on the plot in the previous section. Viewing the video and visualizing the errors on a per-frame basis is therefore crucial in identifying specific failure modes which can be improved by refining the algorithm.
You can use the Ground Truth Labeler app as a visualization tool to view the video containing the ground truth data and the estimated lane boundaries. The driving.connector.Connector
Use the parabolicLaneBoundary array and the ground truth data to compute vehicle coordinate locations of the estimated points. The parabolicLaneBoundary array defines a line, and the ground truth data has discrete points marked on the road. The helperGetCorrespondingPoints function estimates points on the estimated lines that correspond to the same Y-axis distance from the vehicle. This helper function is defined at the end of the example.
The ground truth points and the estimated points are now included in a new timetable to be visualized in the Ground Truth Labeler app. The created groundTruth object is then stored as a MAT file.
% Compute the estimated point locations using the monoCamera. [estVehiclePoints, estImagePoints] = helperGetCorrespondingPoints(monoCameraSensor, ... measurements.LaneBoundaries, ... gtdata.LanesInVehicleCoord, ... assignments); % Add estimated lanes to the measurements timetable. measurements.EstimatedLanes = estImagePoints; measurements.LanesInVehicleCoord = estVehiclePoints; % Create a new timetable with all the variables needed for visualization. names = {'LanePoints'; 'DetectedLanePoints'}; types = labelType({'Line'; 'Line'}); labelDefs = table(names, types, 'VariableNames', {'Name','Type'}); visualizeInFrame = timetable(gtdata.Time, ... gtdata.LaneBoundaries, ... measurements.EstimatedLanes, ... 'VariableNames', names); % Create groundTruth object. dataSource = groundTruthDataSource(videoName); dataToVisualize = groundTruth(dataSource, labelDefs, visualizeInFrame); % Save all the results of the previous section in distanceData.mat in a % temporary folder. dataToLoad = [tempdir 'distanceData.mat']; save(dataToLoad, 'monoSensorHelper', 'videoName', 'measurements', 'gtdata', 'averageDistance');
The helperCustomUI class creates the plot and Bird's-Eye Views using data loaded from a MAT file, like the one you just created. The Connector interface of the Ground Truth Labeler app interacts with the helperCustomUI class through the helperUIConnector class to synchronize the video with the average distance plot and the Bird's-Eye View. This synchronization enables you to analyze per-frame results both analytically and visually.
Follow these steps to visualize the results as shown in the images that follow:
Go to the temporary directory where
distanceData.matis saved and open the Ground Truth Labeler app. Then start the Ground Truth Labeler app, with the connector handle specified ashelperUIConnectorusing the following commands:
>> origdir = pwd;
>> cd(tempdir)
>> groundTruthLabeler(dataSource, 'ConnectorTargetHandle', @helperUIConnector);
Import labels: Visualize the ground truth lane markers and the estimated lanes in the image coordinates. From the app toolstrip, click Import Labels. Then select the From Workspace option and load the
dataToVisualizeground truth into the app. The main app window now contains annotations for lane markers.
You can now navigate through the video and examine the errors. To return back to the original directory, you can type:
>> cd(origdir)
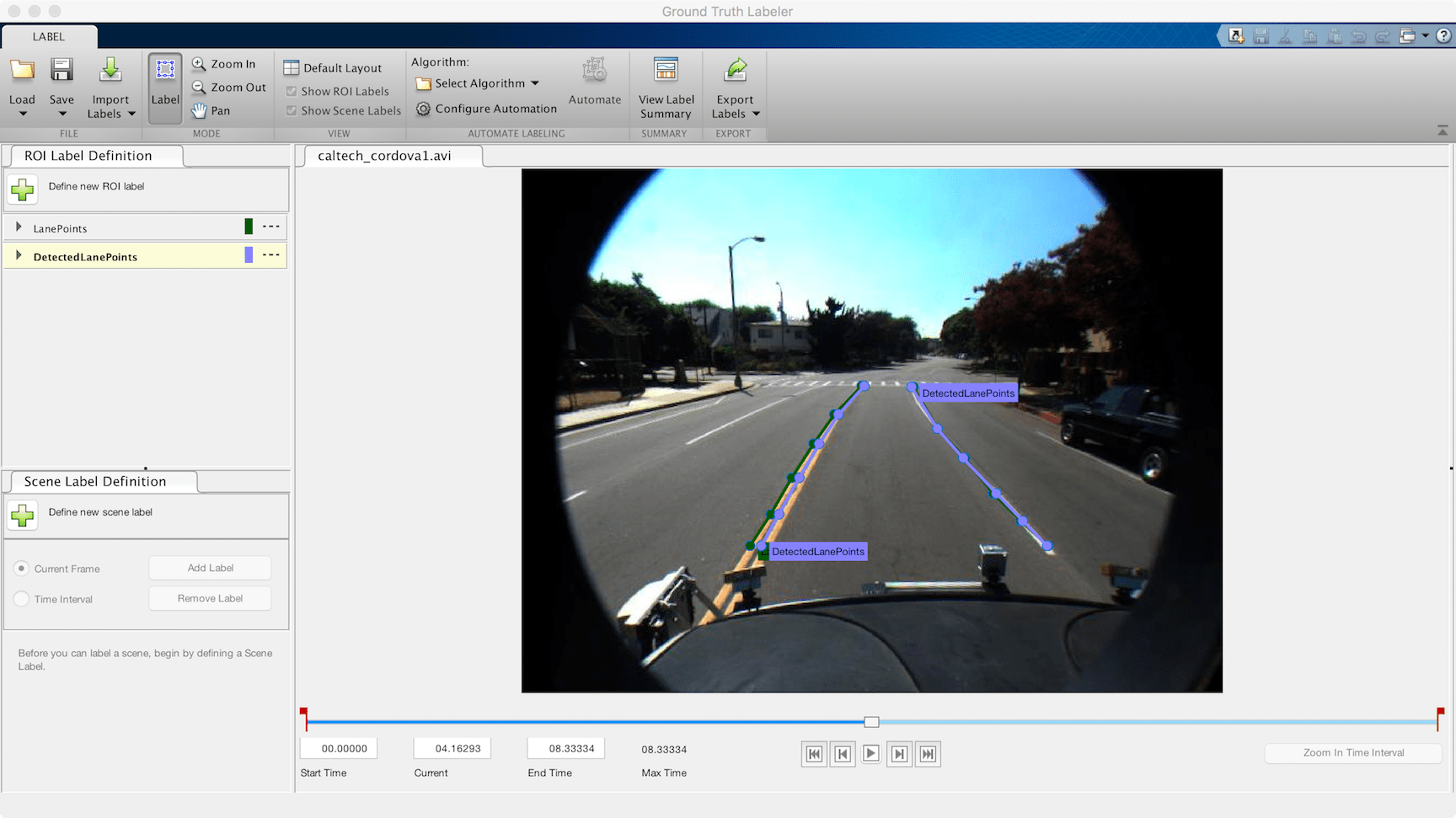


From this visualization, you can make several inferences about the algorithm and the quality of the ground truth data.
The left lane accuracy is consistently worse than the right lane accuracy. Upon closer observation in the Bird's-Eye View display, the ground truth data is marked as the outer boundary of the double line, whereas the estimated lane boundary lays generally at the center of the double line marker. This indicates that the left lane estimation is likely more accurate than the numbers portray, and that a clearly defined ground truth dataset is crucial for such observations.
The detection gaps around 2.3 seconds and 4 seconds correspond to intersections on the road that are preceded by crosswalks. This indicates that the algorithm does not perform well in the presence of crosswalks.
Around 6.8 seconds, as the vehicle approaches a third intersection, the ego lane diverges into a left-only lane and a straight lane. Here too, the algorithm fails to capture the left lane accurately, and the ground truth data also does not contain any information for five frames.
Conclusion
This example showed how to measure the accuracy of a lane boundary detection algorithm and visualize it using the Ground Truth Labeler app. You can extend this concept to other custom algorithms to simplify these workflows and extend the functionality of the app for custom measurements.
Supporting Functions
helperComputeLaneStatistics
This helper function computes statistics for lane boundary detections as compared to ground truth points. It takes in a function handle that can be used to generalize the statistic that needs to be computed, including @mean and @median.
function stat = helperComputeLaneStatistics(estModels, gtPoints, assignments, fcnHandle) numFrames = length(estModels); % Make left and right estimates NaN by default to represent lack of % data. stat = NaN*ones(numFrames, 2); for frameInd = 1:numFrames % Make left and right estimates NaN by default. stat(frameInd, :) = NaN*ones(2, 1); for idx = 1:length(estModels{frameInd}) % Ignore false positive assignments. if assignments{frameInd}(idx) == 0 continue; end % The kth boundary in estModelInFrame is matched to kth % element indexed by assignments in gtPointsInFrame. thisModel = estModels{frameInd}(idx); thisGT = gtPoints{frameInd}{assignments{frameInd}(idx)}; thisGTModel = driving.internal.piecewiseLinearBoundary(thisGT); if mean(thisGTModel.Points(:,2)) > 0 % left lane xPoints = thisGTModel.Points(:,1); yDist = zeros(size(xPoints)); for index = 1:numel(xPoints) gtYPoints = thisGTModel.computeBoundaryModel(xPoints(index)); testYPoints = thisModel.computeBoundaryModel(xPoints(index)); yDist(index) = abs(testYPoints-gtYPoints); end stat(frameInd, 1) = fcnHandle(yDist); else % right lane xPoints = thisGTModel.Points(:,1); yDist = zeros(size(xPoints)); for index = 1:numel(xPoints) gtYPoints = thisGTModel.computeBoundaryModel(xPoints(index)); testYPoints = thisModel.computeBoundaryModel(xPoints(index)); yDist(index) = abs(testYPoints-gtYPoints); end stat(frameInd, 2) = fcnHandle(yDist); end end end end
helperGetCorrespondingPoints
This helper function creates vehicle and image coordinate points at X-axis locations that match the ground truth points.
function [vehiclePoints, imagePoints] = helperGetCorrespondingPoints(monoCameraSensor, estModels, gtPoints, assignments) numFrames = length(estModels); imagePoints = cell(numFrames, 1); vehiclePoints = cell(numFrames, 1); for frameInd = 1:numFrames if isempty(assignments{frameInd}) imagePointsInFrame = []; vehiclePointsInFrame = []; else estModelInFrame = estModels{frameInd}; gtPointsInFrame = gtPoints{frameInd}; imagePointsInFrame = cell(length(estModelInFrame), 1); vehiclePointsInFrame = cell(length(estModelInFrame), 1); for idx = 1:length(estModelInFrame) % Ignore false positive assignments. if assignments{frameInd}(idx) == 0 imagePointsInFrame{idx} = [NaN NaN]; continue; end % The kth boundary in estModelInFrame is matched to kth % element indexed by assignments in gtPointsInFrame. thisModel = estModelInFrame(idx); thisGT = gtPointsInFrame{assignments{frameInd}(idx)}; xPoints = thisGT(:, 1); yPoints = thisModel.computeBoundaryModel(xPoints); vehiclePointsInFrame{idx} = [xPoints, yPoints]; imagePointsInFrame{idx} = vehicleToImage(monoCameraSensor, [xPoints yPoints]); end end vehiclePoints{frameInd} = vehiclePointsInFrame; imagePoints{frameInd} = imagePointsInFrame; % Make imagePoints [] instead of {} to comply with groundTruth object. if isempty(imagePoints{frameInd}) imagePoints{frameInd} = []; end if isempty(vehiclePoints{frameInd}) vehiclePoints{frameInd} = []; end end end
