Analyzing the Response of an RLC Circuit
This example shows how to analyze the time and frequency responses of common RLC circuits as a function of their physical parameters using Control System Toolbox™ functions.
Bandpass RLC Network
The following figure shows the parallel form of a bandpass RLC circuit.

The transfer function from input to output voltage is:
The product LC controls the bandpass frequency while RC controls how narrow the passing band is. To build a bandpass filter tuned to the frequency 1 rad/s, set L=C=1 and use R to tune the filter band.
Analyzing the Frequency Response of the Circuit
The Bode plot is a convenient tool for investigating the bandpass characteristics of the RLC network. Use tf to specify the circuit transfer function for the values R=L=C=1.
R = 1; L = 1; C = 1; G = tf([1/(R*C) 0],[1 1/(R*C) 1/(L*C)])
G =
s
-----------
s^2 + s + 1
Continuous-time transfer function.
Model Properties
Plot the frequency response of the circuit.
bodeplot(G)
grid on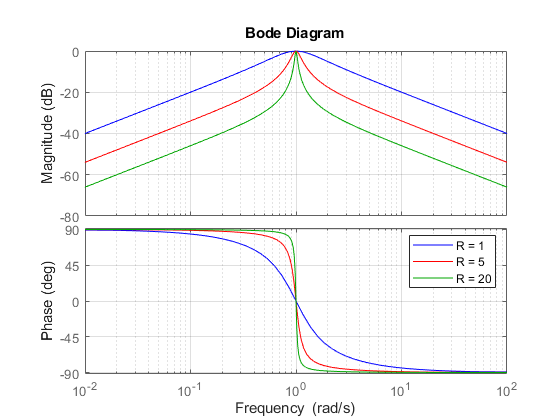
As expected, the RLC filter has maximum gain at the frequency 1 rad/s. However, the attenuation is only -10dB half a decade away from this frequency. To get a narrower passing band, try increasing values of R as follows.
R1 = 5; G1 = tf([1/(R1*C) 0],[1 1/(R1*C) 1/(L*C)]); R2 = 20; G2 = tf([1/(R2*C) 0],[1 1/(R2*C) 1/(L*C)]); bodeplot(G,"b",G1,"r",G2,"g") grid on legend("R = 1","R = 5","R = 20");

The resistor value R=20 gives a filter narrowly tuned around the target frequency of 1 rad/s.
Analyzing the Time Response of the Circuit
We can confirm the attenuation properties of the circuit G2 (R=20) by simulating how this filter transforms sine waves with frequency 0.9, 1, and 1.1 rad/s.
t = 0:0.05:250; subplot(3,1,1) lp1 = lsimplot(G2,sin(t),t); lp1.Title.FontSize = 8; lp1.XLabel.FontSize = 8; lp1.YLabel.FontSize = 8; title("w = 1") subplot(3,1,2) lp2 = lsimplot(G2,sin(0.9*t),t); lp2.Title.FontSize = 8; lp2.XLabel.FontSize = 8; lp2.YLabel.FontSize = 8; title("w = 0.9") subplot(3,1,3) lp3 = lsimplot(G2,sin(1.1*t),t); lp3.Title.FontSize = 8; lp3.XLabel.FontSize = 8; lp3.YLabel.FontSize = 8; title("w = 1.1")

The waves at 0.9 and 1.1 rad/s are considerably attenuated. The wave at 1 rad/s comes out unchanged once the transients have died off. The long transient results from the poorly damped poles of the filters, which unfortunately are required for a narrow passing band.
damp(pole(G2))
Pole Damping Frequency Time Constant
(rad/TimeUnit) (TimeUnit)
-2.50e-02 + 1.00e+00i 2.50e-02 1.00e+00 4.00e+01
-2.50e-02 - 1.00e+00i 2.50e-02 1.00e+00 4.00e+01