lqi
Linear-Quadratic-Integral control
Syntax
[K,S,e] = lqi(SYS,Q,R,N)
Description
lqi computes an optimal state-feedback control
law for the tracking loop shown in the following figure.
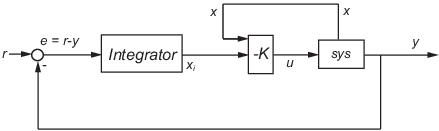
For a plant sys with the state-space equations
(or their discrete counterpart):
the state-feedback control is of the form
where xi is the integrator output. This control law ensures that the output y tracks the reference command r. For MIMO systems, the number of integrators equals the dimension of the output y.
[K,S,e] = lqi(SYS,Q,R,N) calculates
the optimal gain matrix K, given a state-space
model SYS for the plant and weighting matrices Q, R, N.
The control law u = –Kz =
–K[x;xi]
minimizes the following cost functions (for r =
0)
for continuous time
for discrete time
In discrete time, lqi computes the
integrator output xi using
the forward Euler formula
where Ts is the
sample time of SYS.
When you omit the matrix N, N is
set to 0. lqi also returns the solution S of
the associated algebraic Riccati equation and the closed-loop eigenvalues e.
Limitations
For the following state-space system with a plant with augmented integrator:
The problem data must satisfy:
The pair (A,B) must be stabilizable.
R must be positive definite.
must be positive semidefinite (equivalently, ).
must have no unobservable mode on the imaginary axis (or unit circle in discrete time).
Tips
lqi supports descriptor models with nonsingular E.
The output S of lqi is the solution
of the Riccati equation for the equivalent explicit state-space model
References
[1] P. C. Young and J. C. Willems, "An approach to the linear multivariable servomechanism problem", International Journal of Control, Volume 15, Issue 5, May 1972 , pages 961–979.
Version History
Introduced in R2008b