Estimate BER for Hard and Soft Decision Viterbi Decoding

Estimate bit error rate (BER) performance for hard-decision and soft-decision Viterbi decoders in AWGN. Compare the performance to that of an uncoded 64-QAM link.

Set the simulation parameters.

rng default
M = 64;                % Modulation order
k = log2(M);           % Bits per symbol
EbNoVec = (4:10)';     % Eb/No values (dB)
numSymPerFrame = 1000; % Number of QAM symbols per frame

Initialize the BER results vectors.

berEstSoft = zeros(size(EbNoVec)); 
berEstHard = zeros(size(EbNoVec));

Set the trellis structure and traceback depth for a rate 1/2, constraint length 7, convolutional code.

trellis = poly2trellis(7,[171 133]);
tbl = 32;
rate = 1/2;

The main processing loops perform these steps:

• Generate binary data

• Convolutionally encode the data

• Apply QAM modulation to the data symbols. Specify unit average power for the transmitted signal

• Pass the modulated signal through an AWGN channel

• Demodulate the received signal using hard decision and approximate LLR methods. Specify unit average power for the received signal

• Viterbi decode the signals using hard and unquantized methods

• Calculate the number of bit errors

The while loop continues to process data until either 100 errors are encountered or ${10}^7$ bits are transmitted.

for n = 1:length(EbNoVec)
    % Convert Eb/No to SNR
    snrdB = EbNoVec(n) + 10*log10(k*rate);
    % Noise variance calculation for unity average signal power
    noiseVar = 10.^(-snrdB/10);
    % Reset the error and bit counters
    [numErrsSoft,numErrsHard,numBits] = deal(0);
    
    while numErrsSoft < 100 && numBits < 1e7
        % Generate binary data and convert to symbols
        dataIn = randi([0 1],numSymPerFrame*k,1);
        
        % Convolutionally encode the data
        dataEnc = convenc(dataIn,trellis);
        
        % QAM modulate
        txSig = qammod(dataEnc,M, ...
            InputType='bit', ...
            UnitAveragePower=true);
        
        % Pass through AWGN channel
        rxSig = awgn(txSig,snrdB,'measured');
        
        % Demodulate the noisy signal using hard decision (bit) and
        % soft decision (approximate LLR) approaches.
        rxDataHard = qamdemod(rxSig,M, ...
            OutputType='bit', ...
            UnitAveragePower=true);
        rxDataSoft = qamdemod(rxSig,M, ...
            OutputType='approxllr', ...
            UnitAveragePower=true, ...
            NoiseVariance=noiseVar);
        
        % Viterbi decode the demodulated data
        dataHard = vitdec(rxDataHard,trellis,tbl,'cont','hard');
        dataSoft = vitdec(rxDataSoft,trellis,tbl,'cont','unquant');
        
        % Calculate the number of bit errors in the frame. 
        % Adjust for the decoding delay, which is equal to 
        % the traceback depth.
        numErrsInFrameHard = ...
            biterr(dataIn(1:end-tbl),dataHard(tbl+1:end));
        numErrsInFrameSoft = ...
            biterr(dataIn(1:end-tbl),dataSoft(tbl+1:end));
        
        % Increment the error and bit counters
        numErrsHard = numErrsHard + numErrsInFrameHard;
        numErrsSoft = numErrsSoft + numErrsInFrameSoft;
        numBits = numBits + numSymPerFrame*k;

    end
    
    % Estimate the BER for both methods
    berEstSoft(n) = numErrsSoft/numBits;
    berEstHard(n) = numErrsHard/numBits;
end

Plot the estimated hard and soft BER data. Plot the theoretical performance for an uncoded 64-QAM channel.

semilogy(EbNoVec,[berEstSoft berEstHard],'-*')
hold on
semilogy(EbNoVec,berawgn(EbNoVec,'qam',M))
legend('Soft','Hard','Uncoded','location','best')
grid
xlabel('Eb/No (dB)')
ylabel('Bit Error Rate')

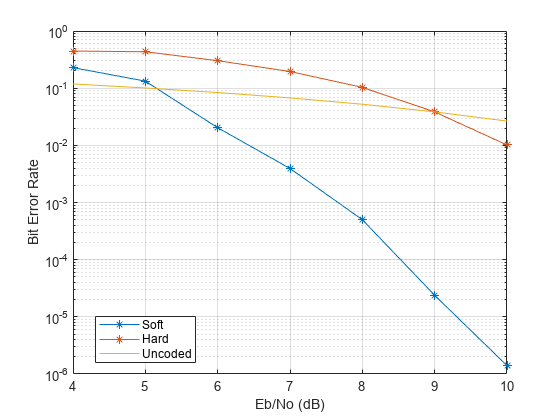
As expected, the soft decision decoding produces the best results.