Bit Error Rate Analysis Techniques
This topic describes how to compute error statistics for various communications systems.
Computation of Theoretical Error Statistics
The biterr function, discussed in the
Compute SERs and BERs Using Simulated Data section, can help you gather empirical error
statistics, but validating your results by comparing them to the theoretical error
statistics is good practice. For certain types of communications systems,
closed-form expressions exist for the computation of the bit error rate (BER) or an
approximate bound on the BER. The functions listed in this table compute the
closed-form expressions for the BER or a bound on it for the specified types of
communications systems.
| Type of Communications System | Function |
|---|---|
| Uncoded AWGN channel | berawgn
|
| Uncoded Rayleigh and Rician fading channel | berfading
|
| Coded AWGN channel | bercoding |
| Uncoded AWGN channel with imperfect synchronization | bersync
|
The analytical expressions used in these functions are discussed in Analytical Expressions Used in BER Analysis. The reference pages of these functions also list references to one or more books containing the closed-form expressions implemented by the function.
Theoretical Performance Results
Plot Theoretical Error Rates
This example uses the bercoding function to compute upper bounds on BERs for convolutional coding with a soft-decision decoder.
coderate = 1/4; % Code rateCreate a structure, dspec, with information about the distance spectrum. Define the energy per bit to noise power spectral density ratio () sweep range and generate the theoretical bound results.
dspec.dfree = 10; % Minimum free distance of code dspec.weight = [1 0 4 0 12 0 32 0 80 0 192 0 448 0 1024 ... 0 2304 0 5120 0]; % Distance spectrum of code EbNo = 3:0.5:8; berbound = bercoding(EbNo,'conv','soft',coderate,dspec);
Plot the theoretical bound results.
semilogy(EbNo,berbound) xlabel('E_b/N_0 (dB)'); ylabel('Upper Bound on BER'); title('Theoretical Bound on BER for Convolutional Coding'); grid on;

Compare Theoretical and Empirical Error Rates
Using the berawgn function, compute the theoretical symbol error rates (SERs) for pulse amplitude modulation (PAM) over a range of values. Simulate 8 PAM with an AWGN channel, and compute the empirical SERs. Compare the theoretical and then empirical SERs by plotting them on the same set of axes.
Compute and plot the theoretical SER using berawgn.
rng('default') % Set random number seed for repeatability M = 8; EbNo = 0:13; [ber,ser] = berawgn(EbNo,'pam',M); semilogy(EbNo,ser,'r'); legend('Theoretical SER'); title('Theoretical Error Rate'); xlabel('E_b/N_0 (dB)'); ylabel('Symbol Error Rate'); grid on;

Compute the empirical SER by simulating an 8 PAM communications system link. Define simulation parameters and preallocate variables needed for the results. As described in [1], because , add 3 dB to the value when converting values to SNR values.
n = 10000; % Number of symbols to process k = log2(M); % Number of bits per symbol snr = EbNo+3+10*log10(k); % In dB ynoisy = zeros(n,length(snr)); z = zeros(n,length(snr)); errVec = zeros(3,length(EbNo));
Create an error rate calculator System object™ to compare decoded symbols to the original transmitted symbols.
errcalc = comm.ErrorRate;
Generate a random data message and apply PAM. Normalize the channel to the signal power. Loop the simulation to generate error rates over the range of SNR values.
x = randi([0 M-1],n,1); % Create message signal y = pammod(x,M); % Modulate signalpower = (real(y)'*real(y))/length(real(y)); for jj = 1:length(snr) reset(errcalc) ynoisy(:,jj) = awgn(real(y),snr(jj),'measured'); % Add AWGN z(:,jj) = pamdemod(complex(ynoisy(:,jj)),M); % Demodulate errVec(:,jj) = errcalc(x,z(:,jj)); % Compute SER from simulation end
Compare the theoretical and empirical results.
hold on; semilogy(EbNo,errVec(1,:),'b.'); legend('Theoretical SER','Empirical SER'); title('Comparison of Theoretical and Empirical Error Rates'); hold off;

Performance Results via Simulation
Section Overview
This section describes how to compare the data messages that enter and leave a communications system simulation and how to compute error statistics using the Monte Carlo technique. Simulations can measure system performance by using the data messages before transmission and after reception to compute the BER or SER for a communications system. To explore physical layer components used to model and simulate communications systems, see PHY Components.
Curve fitting can be useful when you have a small or imperfect data set but want to plot a smooth curve for presentation purposes. To explore the use of curve fitting when computing performance results via simulation, see the Curve Fitting for Error Rate Plots section.
Compute SERs and BERs Using Simulated Data
The example shows how to compute SERs and BERs using the biterr and symerr functions, respectively. The symerr function compares two sets of data and computes the number of symbol errors and the SER. The biterr function compares two sets of data and computes the number of bit errors and the BER. An error is a discrepancy between corresponding points in the two sets of data.
The two sets of data typically represent messages entering a transmitter and recovered messages leaving a receiver. You can also compare data entering and leaving other parts of your communications system (for example, data entering an encoder and data leaving a decoder).
If your communications system uses several bits to represent one symbol, counting symbol errors is different from counting bit errors. In either the symbol- or bit-counting case, the error rate is the number of errors divided by the total number of transmitted symbols or bits, respectively.
Typically, simulating enough data to produce at least 100 errors provides accurate error rate results. If the error rate is very small (for example, or less), using the semianalytic technique might compute the result more quickly than using a simulation-only approach. For more information, see the Performance Results via Semianalytic Technique section.
Compute Error Rates
Use the symerr function to compute the SERs for a noisy linear block code. Apply no digital modulation, so that each symbol contains a single bit. When each symbol is a single bit, the symbol errors and bit errors are the same.
After artificially adding noise to the encoded message, compare the resulting noisy code to the original code. Then, decode and compare the decoded message to the original message.
m = 3; % Set parameters for Hamming code n = 2^m-1; k = n-m; msg = randi([0 1],k*200,1); % Specify 200 messages of k bits each code = encode(msg,n,k,'hamming'); codenoisy = bsc(code,0.95); % Add noise newmsg = decode(codenoisy,n,k,'hamming'); % Decode and correct errors
Compute the SERs.
[~,noisyVec] = symerr(code,codenoisy); [~,decodedVec] = symerr(msg,newmsg);
The error rate decreases after decoding because the Hamming decoder correct errors based on the error-correcting capability of the decoder configuration. Because random number generators produce the message and noise is added, results vary from run to run. Display the SERs.
disp(['SER in the received code: ',num2str(noisyVec(1))])SER in the received code: 0.94571
disp(['SER after decoding: ',num2str(decodedVec(1))])SER after decoding: 0.9675
Comparing SER and BER
These commands show the difference between symbol errors and bit errors in various situations.
Create two three-element decimal vectors and show the binary representation. The vector a contains three 2-bit symbols, and the vector b contains three 3-bit symbols.
bpi = 3; % Bits per integer
a = [1 2 3];
b = [1 4 4];
int2bit(a,bpi)ans = 3×3
0 0 0
0 1 1
1 0 1
int2bit(b,bpi)
ans = 3×3
0 1 1
0 0 0
1 0 0
Compare the binary values of the two vectors and compute the number of errors and the error rate by using the biterr and symerr functions.
format rat % Display fractions instead of decimals [snum,srate] = symerr(a,b)
snum =
2
srate =
2/3
snum is 2 because the second and third entries have bit differences. srate is 2/3 because the total number of symbols is 3.
[bnum,brate] = biterr(a,b)
bnum =
5
brate =
5/9
bnum is 5 because the second entries differ in two bits, and the third entries differ in three bits. brate is 5/9 because the total number of bits is 9. By definition, the total number of bits is the number of entries in a for symbol error computations or b for bit error computations times the maximum number of bits among all entries of a and b, respectively.
Performance Results via Semianalytic Technique
The technique described in the Performance Results via Simulation section can work for a large variety of communications systems but can be prohibitively time-consuming for small error rates (for example, 10-6 or less). The semianalytic technique is an alternative way to compute error rates. The semianalytic technique can produce results faster than a nonanalytic method that uses simulated data.
For more information on implementing the semianalytic technique using a
combination of simulation and analysis to determine the error rate of a
communications system, see the semianalytic function.
Error Rate Plots
Section Overview
Error rate plots can be useful when examining the performance of a communications system and are often included in publications. This section discusses and demonstrates tools you can use to create error rate plots, modify them to suit your needs, and perform curve fitting on the error rate data and the plots.
Creation of Error Rate Plots Using semilogy Function
In many error rate plots, the horizontal axis indicates
Eb/N0
values in dB, and the vertical axis indicates the error rate using a logarithmic
(base 10) scale. For examples that create such a plot using the semilogy function, see Compare Theoretical and Empirical Error Rates and Plot Theoretical Error Rates.
Curve Fitting for Error Rate Plots
Curve fitting can be useful when you have a small or imperfect data set but
want to plot a smooth curve for presentation purposes. The berfit function includes
curve-fitting capabilities that help your analysis when the empirical data
describes error rates at different
Eb/N0
values. This function enables you to:
Customize various relevant aspects of the curve-fitting process, such as a list of selections for the type of closed-form function used to generate the fit.
Plot empirical data along with a curve that
berfitfits to the data.Interpolate points on the fitted curve between Eb/N0 values in your empirical data set to smooth the plot.
Collect relevant information about the fit, such as the numerical values of points along the fitted curve and the coefficients of the fit expression.
Note
The berfit function is
intended for curve fitting or interpolation, not extrapolation.
Extrapolating BER data beyond an order of magnitude below the smallest
empirical BER value is inherently unreliable.
Use Curve Fitting on Error Rate Plot
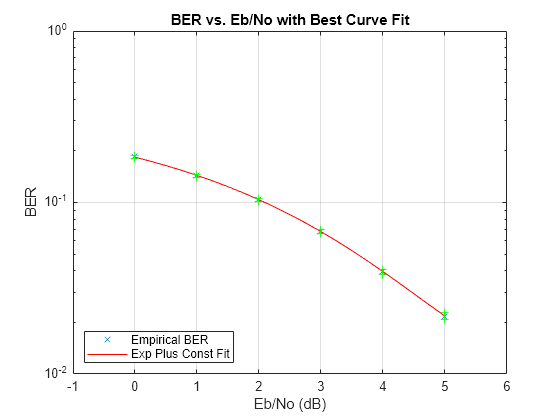
This example simulates a simple differential binary phase shift keying (DBPSK) communications system and plots error rate data for a series of values. It uses the berfit and berconfint functions to fit a curve to a set of empirical error rates.
Initialize Simulation Parameters
Specify the input signal message length, modulation order, range of values to simulate, and the minimum number of errors that must occur before the simulation computes an error rate for a given value. Preallocate variables for final results and interim results.
Typically, for statistically accurate error rate results, the minimum number of errors must be on the order of 100. This simulation uses a small number of errors to shorten the run time and to illustrate how curve fitting can smooth a set of results.
siglen = 100000; % Number of bits in each trial M = 2; % DBPSK is binary EbN0vec = 0:5; % Vector of EbN0 values minnumerr = 5; % Compute BER after only 5 errors occur numEbN0 = length(EbN0vec); % Number of EbN0 values ber = zeros(1,numEbN0); % Final BER values berVec = zeros(3,numEbN0); % Updated BER values intv = cell(1,numEbN0); % Cell array of confidence intervals
Create an error rate calculator System object™.
errorCalc = comm.ErrorRate;
Loop the Simulation
Simulate the DBPSK-modulated communications system and compute the BER using a for loop to vary the value. The inner while loop ensures that a minimum number of bit errors occur for each value. Error rate statistics are saved for each value and used later in this example when curve fitting and plotting.
for jj = 1:numEbN0 EbN0 = EbN0vec(jj); snr = EbN0; % For binary modulation SNR = EbN0 reset(errorCalc) while (berVec(2,jj) < minnumerr) msg = randi([0,M-1],siglen,1); % Generate message sequence txsig = dpskmod(msg,M); % Modulate rxsig = awgn(txsig,snr,'measured'); % Add noise decodmsg = dpskdemod(rxsig,M); % Demodulate berVec(:,jj) = errorCalc(msg,decodmsg); % Calculate BER end
Use the berconfint function to compute the error rate at a 98% confidence interval for the values.
[ber(jj),intv1] = berconfint(berVec(2,jj),berVec(3,jj),0.98);
intv{jj} = intv1;
disp(['EbN0 = ' num2str(EbN0) ' dB, ' num2str(berVec(2,jj)) ...
' errors, BER = ' num2str(ber(jj))])
endEbN0 = 0 dB, 18427 errors, BER = 0.18427 EbN0 = 1 dB, 14322 errors, BER = 0.14322 EbN0 = 2 dB, 10384 errors, BER = 0.10384 EbN0 = 3 dB, 6789 errors, BER = 0.06789 EbN0 = 4 dB, 3945 errors, BER = 0.03945 EbN0 = 5 dB, 2175 errors, BER = 0.02175
Use the berfit function to plot the best fitted curve, interpolating between BER points to get a smooth plot. Add confidence intervals to the plot.
fitEbN0 = EbN0vec(1):0.25:EbN0vec(end); % Interpolation values berfit(EbN0vec,ber,fitEbN0); hold on; for jj=1:numEbN0 semilogy([EbN0vec(jj) EbN0vec(jj)],intv{jj},'g-+'); end hold off;