Frequency Correction for ADALM-PLUTO Radio in Simulink
This example shows how to synchronize both the baseband sample rate and the center frequency of two PlutoSDRs by using the Frequency correction parameter of the ADALM-PLUTO Radio Receiver block.
The baseband sample rate and the center frequency of a PlutoSDR are physically derived from the same oscillator. Although each PlutoSDR is factory-calibrated to use appropriate PLL settings to digitally compensate for component variations of the oscillator, the compensation is imperfect because of quantization effects and changes in operating conditions (temperature in particular). Consequently, two PlutoSDRs will operate at slightly different baseband sample rates and center frequencies even if the corresponding System objects or Simulink blocks for the two PlutoSDRs use the same baseband sample rate and the same center frequency. To solve this problem, the Frequency correction parameter of the ADALM-PLUTO Radio Receiver block can be used.
The Frequency correction parameter specifies the parts-per-million change to the baseband sample rate and the center frequency. The default value is 0, which means that the radio will use its factory-calibrated PLL settings. In this example, we treat one PlutoSDR, the transmitter, as a source with accurate baseband sample rate and center frequency. We use the signal received by another PlutoSDR, the receiver, to estimate the right value of Frequency correction for the receiver block, and show that when Frequency correction is set appropriately, the frequency of the received tone will be very close to 80 kHz, the frequency of the transmitted tone.
Refer to the Getting Started documentation for details on configuring your host computer to work with the PlutoSDR.
Algorithm for Estimating Frequency Correction
Consider a signal transmitted from one PlutoSDR to another PlutoSDR. Let  and
and  be the center frequency and the baseband sample rate of the transmitter. Let
be the center frequency and the baseband sample rate of the transmitter. Let 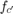 and
and 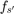 be the center frequency and the baseband sample rate of the receiver. Assume that the oscillator of the transmitter has not drifted and the oscillator of the receiver has drifted by a factor
be the center frequency and the baseband sample rate of the receiver. Assume that the oscillator of the transmitter has not drifted and the oscillator of the receiver has drifted by a factor  , i.e.
, i.e. 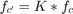 and
and 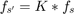 where
where  is a number very close to 1.
is a number very close to 1.
A tone at baseband frequency 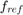 in the transmitted signal will appear as a tone at baseband frequency
in the transmitted signal will appear as a tone at baseband frequency  in the receiver, where
in the receiver, where 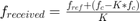 . The term
. The term  in the numerator is due to the mismatch in center frequencies. The scaling factor
in the numerator is due to the mismatch in center frequencies. The scaling factor  in the denominator is due to the mismatch in baseband sample rates. Hence, we can solve for
in the denominator is due to the mismatch in baseband sample rates. Hence, we can solve for  with
with 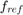 ,
,  , and
, and 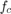 .
. 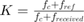 .
.
To remove the frequency offset between the transmitter and the receiver, we need to scale the baseband sample rate and the center frequency of the receiver by a factor of 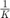 . Let
. Let  be the parts-per-million change to the baseband sample rate and the center frequency of the receiver. Then
be the parts-per-million change to the baseband sample rate and the center frequency of the receiver. Then 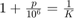 . Therefore
. Therefore 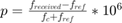 .
.
Set up the Transmitter and the Receiver
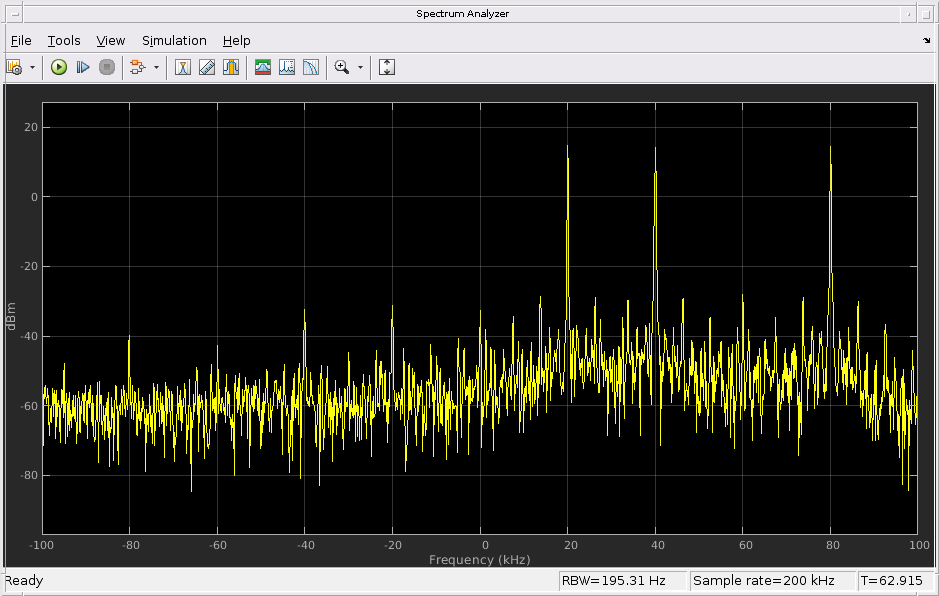
We use one PlutoSDR to transmit three tones at 20, 40, and 80 kHz. The tone at 80 kHz is used to estimate the value for Frequency correction for the receiver. The tones at 20 and 40 kHz are only used to help visualize the spectrum.
% Set up parameters and signals sampleRate = 200e3; centerFreq = 2.42e9; fRef = 80e3; s1 = exp(1j*2*pi*20e3*[0:10000-1]'/sampleRate); % 20 kHz s2 = exp(1j*2*pi*40e3*[0:10000-1]'/sampleRate); % 40 kHz s3 = exp(1j*2*pi*fRef*[0:10000-1]'/sampleRate); % 80 kHz s = s1 + s2 + s3; s = 0.6*s/max(abs(s)); % Scale signal to avoid clipping in the time domain % Set up the transmitter % Use the default value of 0 for FrequencyCorrection, which corresponds to % the factory-calibrated condition tx = sdrtx('Pluto', 'RadioID', 'usb:1', 'CenterFrequency', centerFreq, ... 'BasebandSampleRate', sampleRate, 'Gain', 0, ... 'ShowAdvancedProperties', true); % Use the info method to show the actual values of various hardware-related % properties txRadioInfo = info(tx) % Send signals disp('Send 3 tones at 20, 40, and 80 kHz'); transmitRepeat(tx, s); % Open the receiver model open_system('plutoradioFrequencyCorrectionRx') % Run the receiver. The detected frequency may be far from 80 kHz disp('Running the receiver...'); sim('plutoradioFrequencyCorrectionRx') disp(['The detected frequency is ' num2str(peakFreq/1000) ' kHz.']);
## Establishing connection to hardware. This process can take several seconds.
txRadioInfo =
struct with fields:
Status: 'Full information'
CenterFrequency: 2.4200e+09
BasebandSampleRate: 200000
SerialNum: '1000002355237309002300260902167028'
Gain: 0
RadioFirmwareVersion: "0.30"
ExpectedFirmwareVersion: "0.30"
HardwareVersion: "A0"
FrequencyCorrection: 0
Send 3 tones at 20, 40, and 80 kHz
## Establishing connection to hardware. This process can take several seconds.
## Waveform transmission has started successfully and will repeat indefinitely.
## Call the release method to stop the transmission.
Running the receiver...
## Establishing connection to hardware. This process can take several seconds.
The detected frequency is 68.0386 kHz.


Estimate the Frequency Correction Value
additionalCorrection = (peakFreq - fRef) / (centerFreq + fRef) * 1e6;
Apply the Frequency Correction Value
Since  , applying two changes
, applying two changes 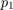 and
and  successively is equivalent to applying a single change of
successively is equivalent to applying a single change of 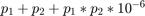 with respect to the factory-calibrated condition.
with respect to the factory-calibrated condition.
currentFrequencyCorrection = str2double( ... get_param('plutoradioFrequencyCorrectionRx/ADALM-Pluto Radio Receiver', ... 'FrequencyCorrection')) newFrequencyCorrection = currentFrequencyCorrection + additionalCorrection + ... currentFrequencyCorrection*additionalCorrection*1e-6 set_param('plutoradioFrequencyCorrectionRx/ADALM-Pluto Radio Receiver', ... 'FrequencyCorrection',num2str(newFrequencyCorrection,'%.12f'))
currentFrequencyCorrection =
0
newFrequencyCorrection =
-4.9426
Verify the Results
Run the receiver again. The detected frequency should be closer to 80 kHz.
disp('Running the receiver again...'); sim('plutoradioFrequencyCorrectionRx') disp(['The detected frequency is ' num2str(peakFreq/1000) ' kHz.']); % Release the transmitter radio release(tx);
Running the receiver again... ## Establishing connection to hardware. This process can take several seconds. The detected frequency is 80.04 kHz.