maxflow
Maximum flow in graph
Syntax
Description
mf = maxflow(G,s,t)s and t. If graph G
is unweighted (that is, G.Edges does not contain the variable
Weight), then maxflow treats all graph
edges as having a weight equal to 1.
Examples
Maximum Flow in Graph
Create and plot a weighted graph. The weighted edges represent flow capacities.
s = [1 1 2 2 3 4 4 4 5 5]; t = [2 3 3 4 5 3 5 6 4 6]; weights = [0.77 0.44 0.67 0.75 0.89 0.90 2 0.76 1 1]; G = digraph(s,t,weights); plot(G,'EdgeLabel',G.Edges.Weight,'Layout','layered');
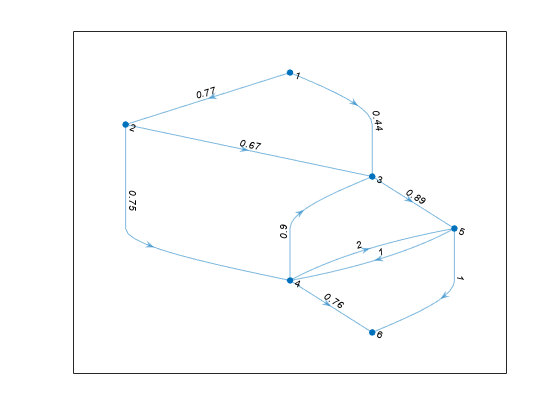
Determine the maximum flow from node 1 to node 6.
mf = maxflow(G,1,6)
mf = 1.2100
Maximum Flow with Specified Algorithm
Create and plot a graph. The weighted edges represent flow capacities.
s = [1 1 2 2 3 3 4];
t = [2 3 3 4 4 5 5];
weights = [10 6 15 5 10 3 8];
G = digraph(s,t,weights);
H = plot(G,'EdgeLabel',G.Edges.Weight);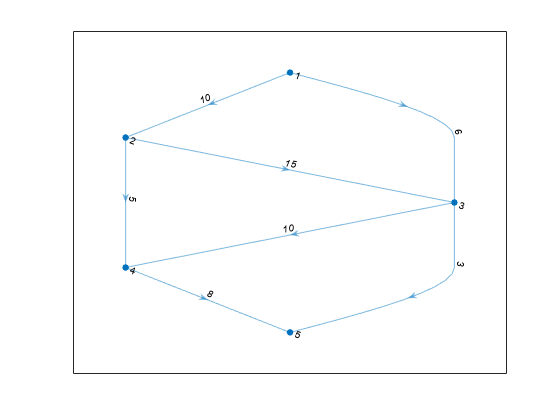
Find the maximum flow value between node 1 and node 5. Specify 'augmentpath' to use the Ford-Fulkerson algorithm, and use two outputs to return a graph of the nonzero flows.
[mf,GF] = maxflow(G,1,5,'augmentpath')mf = 11
GF =
digraph with properties:
Edges: [6x2 table]
Nodes: [5x0 table]
Highlight and label the graph of nonzero flows.
H.EdgeLabel = {};
highlight(H,GF,'EdgeColor','r','LineWidth',2);
st = GF.Edges.EndNodes;
labeledge(H,st(:,1),st(:,2),GF.Edges.Weight);
Minimum Cut Computation
Create and plot a weighted graph. The edge weights represent flow capacities.
s = [1 1 2 3 3 4 4 5 5]; t = [2 3 3 2 5 5 6 4 6]; weights = [0.77 0.44 0.67 0.69 0.73 2 0.78 1 1]; G = digraph(s,t,weights); plot(G,'EdgeLabel',G.Edges.Weight,'Layout','layered')
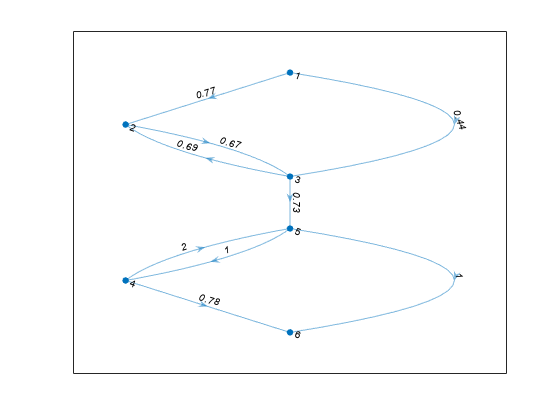
Find the maximum flow and minimum cut of the graph.
[mf,~,cs,ct] = maxflow(G,1,6)
mf = 0.7300
cs = 3×1
1
2
3
ct = 3×1
4
5
6
Plot the minimum cut, using the cs nodes as sources and the ct nodes as sinks. Highlight the cs nodes as red and the ct nodes as green. Note that the weight of the edge that connects these two sets of nodes is equal to the maximum flow.
H = plot(G,'Layout','layered','Sources',cs,'Sinks',ct, ... 'EdgeLabel',G.Edges.Weight); highlight(H,cs,'NodeColor','red') highlight(H,ct,'NodeColor','green')
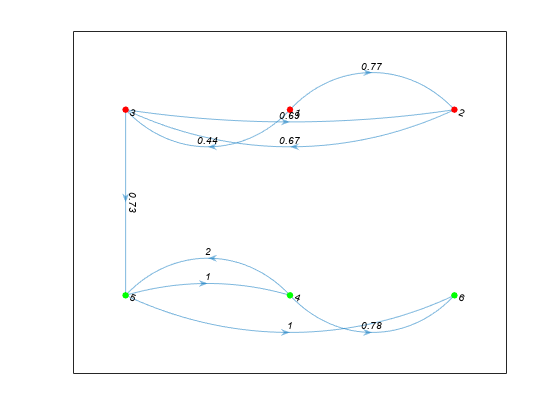
Input Arguments
s,t — Node pair (as separate arguments)
node indices | node names
Node pair, specified as separate arguments of node indices or node names to indicate the source node and target node. This table shows the different ways to refer to nodes either by their node indices or by their node names.
| Value | Example |
|---|---|
| Scalar node index | 1 |
| Character vector node name | 'A' |
| String scalar node name | "A" |
Example: mf = maxflow(G,'A','B')
Example: mf = maxflow(G,1,10)
Data Types: double | char | string
algorithm — Maximum flow algorithm
'searchtrees' (default) | 'augmentpath' | 'pushrelabel'
Maximum flow algorithm, specified as one of the entries in the table.
Note
You can only specify nondefault algorithm options
with a directed graph.
| Option | Description |
|---|---|
'searchtrees' (default) |
Uses the Boykov-Kolmogorov algorithm. Computes the
maximum flow by constructing two search trees associated
with nodes |
'augmentpath' |
Uses the Ford-Fulkerson algorithm. Computes the maximum flow iteratively by finding an augmenting path in a residual directed graph. The directed graph cannot have any parallel edges of
opposite direction between the same two nodes, unless
the weight of one of those edges is zero. So if the
graph contains edge |
'pushrelabel' |
Computes the maximum flow by pushing a node's excess flow to its neighbors and then relabeling the node. The directed graph cannot have any parallel edges of
opposite direction between the same two nodes, unless
the weight of one of those edges is zero. So if the
graph contains edge |
Example: mf =
maxflow(G,'A','D','augmentpath')
Output Arguments
mf — Maximum flow
scalar
Maximum flow, returned as a scalar.
GF — Directed graph of flows
digraph object
Directed graph of flows, returned as a digraph object.
GF contains the same nodes as G,
but only contains those edges of G that have a nonzero
flow. For multigraphs with multiple edges between the same two nodes,
GF contains a single edge reflecting the flow through
the multiple edges.
cs — Minimum cut source node IDs
node indices | node names
Minimum cut source node IDs, returned as node indices or node names.
If
sandtspecify numeric node indices, thencsandctalso contain node indices.If
sandtspecify node names, thencsandctalso contain node names.
ct — Minimum cut target node IDs
scalar | vector | character vector | cell array of character vectors
Minimum cut target node IDs, returned as node indices or node names.
If
sandtspecify numeric node indices, thencsandctalso contain node indices.If
sandtspecify node names, thencsandctalso contain node names.
More About
Maximum Flow
In the context of maximum flow, the edges in a graph are
considered to have a capacity as represented by the edge
weight. The capacity of an edge is the amount of flow that can pass through that
edge. Therefore, the maximum flow between two nodes in a graph maximizes the amount
of flow passing from the source node, s, to the target node,
t, based on the capacities of the connecting edges.
Minimum Cut
A minimum cut partitions the directed graph nodes into two sets,
cs and ct, such that the sum of the
weights of all edges connecting cs and ct
(weight of the cut) is minimized. The weight of the minimum cut is equal to the
maximum flow value, mf.
The entries in cs and ct indicate the nodes
of G associated with nodes s and
t, respectively. cs and
ct satisfy numel(cs) + numel(ct) =
numnodes(G).
Extended Capabilities
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
Version History
Introduced in R2015b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)