Vehicle Body 1DOF Longitudinal
Two-axle vehicle in forward and reverse motion
Libraries:
Powertrain Blockset /
Vehicle Dynamics
Vehicle Dynamics Blockset /
Vehicle Body
Description
The Vehicle Body 1DOF Longitudinal block implements a one degree-of-freedom (1DOF) rigid vehicle body with constant mass undergoing longitudinal (that is, forward and reverse) motion. Use the block:
In powertrain and fuel economy studies to represent the vehicle inertial and drag loads when weight transfer from vertical and pitch motions are negligible.
To determine the engine torque and power required for the vehicle to follow a specified drive cycle.
You can select block options to create input ports for external forces, moments, air temperature, and wind speed.
| Block Option Setting | External Input Ports | Description |
|---|---|---|
External forces |
| External force applied to vehicle CG in the vehicle-fixed frame. |
External moments |
| External moment about vehicle CG in the vehicle-fixed frame. |
Air temperature |
| Ambient air temperature. Consider this option if you want to vary the temperature during run-time. |
Wind X,Y,Z |
| Wind speed along earth-fixed X-, Y-, and Z-axes. If
you do not select this option, the block implements input port
|
Vehicle Body Model
The vehicle axles are parallel and form a plane. The longitudinal direction lies in this plane and is perpendicular to the axles. If the vehicle is traveling on an inclined slope, the normal direction is not parallel to gravity but is always perpendicular to the axle-longitudinal plane.
The block uses the net effect of all the forces and torques acting on it to determine the vehicle motion. The longitudinal tire forces push the vehicle forward or backward. The weight of the vehicle acts through its center of gravity (CG). The grade angle changes the direction of the resolved gravitational force acting on the vehicle CG. Similarly, the block resolves the resistive aerodynamic drag force on the vehicle CM.
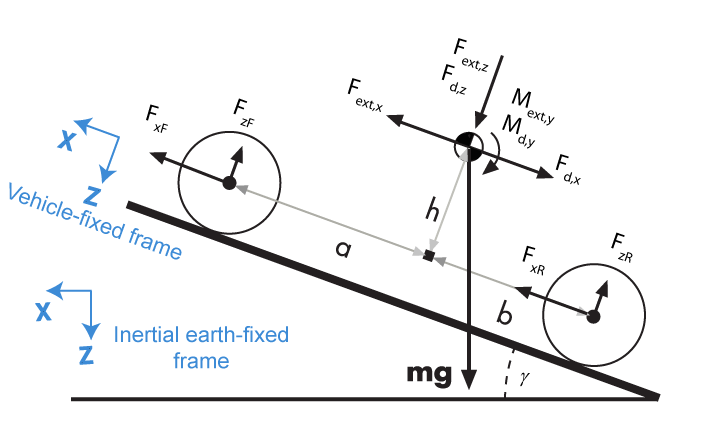
The Vehicle Body 1DOF Longitudinal block implements these equations.
Zero normal acceleration and zero pitch torque determine the normal force on each front and rear axles.
The wheel normal forces satisfy this equation.
Wind and Drag Forces
The block subtracts the wind speeds from the vehicle velocity components to obtain a net relative airspeed. To calculate the drag force and moments acting on the vehicle, the block uses the net relative airspeed.
By default, to calculate the wind speed along the vehicle-fixed x-axis, the block uses the longitudinal wind speed along the earth-fixed X-axis. If you select WindX,Y,Z, the block uses the wind speed along the earth-fixed X-, Y-, Z-axes.
Power Accounting
For the power accounting, the block implements these equations.
| Bus Signal | Description | Equations | ||
|---|---|---|---|---|
|
|
| Externally applied force power | |
| Longitudinal force power applied at the front axle | |||
| Longitudinal force power applied at the rear axle | |||
|
|
| Drag force power | ||
|
|
| Rate change in gravitational potential energy | ||
| Rate in change of longitudinal kinetic energy | |||
The equations use these variables.
| Fxf, Fxr | Longitudinal forces on each wheel at the front and rear ground contact points, respectively |
| Fzf, Fzr | Normal load forces on each wheel at the front and rear ground contact points, respectively |
| FwF, FwR | Longitudinal force on front and rear axles along vehicle-fixed x-axis |
| FxExt, FwR | External force along the vehicle-fixed x-axis |
| Fd,x, Fd,z | Longitudinal and normal drag force on vehicle CG |
| Md,y | Torque due to drag on vehicle about the vehicle-fixed y-axis |
| Fd | Aerodynamic drag force |
| Vx | Velocity of the vehicle. When Vx > 0, the vehicle moves forward. When Vx < 0, the vehicle moves backward. |
| Nf, Nr | Number of wheels on front and rear axle, respectively |
Angle of road grade | |
| m | Vehicle body mass |
| a,b | Distance of front and rear axles, respectively, from the normal projection point of vehicle CG onto the common axle plane |
| h | Height of vehicle CG above the axle plane |
| Cd | Frontal air drag coefficient |
| Af | Frontal area |
| Pabs | Absolute pressure |
| ρ | Mass density of air |
| x, , | Vehicle longitudinal position, velocity, and acceleration along the vehicle-fixed x-axis |
| wx | Wind speed along the vehicle-fixed x-axis |
Vehicle vertical velocity along the vehicle-fixed z-axis |
Limitations
The Vehicle Body 1DOF Longitudinal block lets you model only longitudinal dynamics, parallel to the ground and oriented along the direction of motion. The vehicle is assumed to be in pitch and normal equilibrium. The block does not model pitch or vertical movement. To model a vehicle with three degrees-of-freedom (DOF), use the Vehicle Body 3DOF Longitudinal.
Ports
Input
Output
Parameters
Extended Capabilities
Version History
Introduced in R2017a