Multiband Nature and Miniaturization of Fractal Antennas

Open Script

This example shows how to analyze the multi band characteristics of fractal antennas and compare the size of fractal antennas with conventional antennas. The term fractal means irregular fragment. A Fractal is a rough or fragmented geometric shape that can be subdivided in parts, each of which is a reduced size of the whole. Fractal geometries are applied to antenna elements which aids in creating antennas of compact size and multi band behavior. These characteristics are required in small and complex circuits. Fractal antennas are multiband, high gain, low profile antennas. They are compact relative to the conventional antennas because of their efficient space filling nature.

The geometry generating process of a fractal begins with a basic geometry referred to as the initiator. The final fractal geometry is an infinitely intricate underlying structure such that no matter how closely the structure is viewed, the fundamental building blocks cannot be differentiated because they are scaled versions of the initiator. Different fractal antennas are koch dipole, koch loop, snowflake, seirpinski carpet, seirpinski gasket and fractal Island.

Koch Curve

A line of unit length is taken, middle third is removed and replaced with two lines of same length as removed one. These two lines and the segment removed should make up an equilateral triangle. This is first iteration. Same procedure is repeated with all the lines for next iterations. Each smaller segment is exact replica of the whole curve. Each iteration adds length to the total curve which results in total length that is (4/3)^n times the original length, where n is number of iterations.

Fractal Koch Dipole Vs Dipole Antenna

Create a dipole with length 60 mm and plot the impedance over the frequency range of 0.5 GHz-5 GHz.

d = dipole('Length',60e-3,'Width',1e-3);
figure;impedance(d,(0.5:0.05:5)*1e9);

The resonant frequency of dipole antenna is 2.35 GHz.

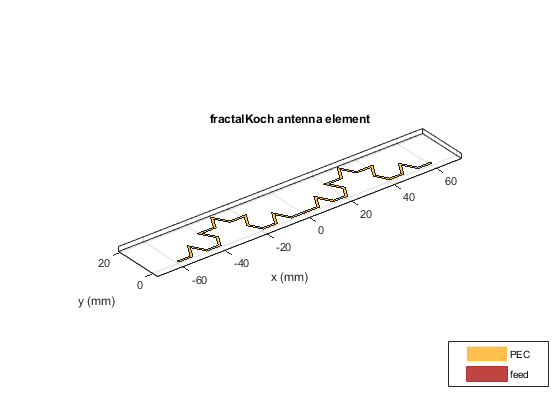
Create a fractal koch dipole. By default, the length is 60 mm and number of iterations are two.

k = fractalKoch;
figure;show(k);

Calculate the impedance over the frequency range of 0.5 GHz-5 GHz.

zk1 = impedance(k,(0.5:0.05:5)*1e9);

Increase the number of iterations to four and calculate the impedance. Plot the impedance for second and fourth iterations.

k.NumIterations = 4;
k.Width = 0.5*k.Width;
zk2 = impedance(k,(0.5:0.05:5)*1e9);
figure;plot((0.5:0.05:5)*1e9,real(zk1),'b',(0.5:0.05:5)*1e9,imag(zk1),'r');grid on;
hold on;plot((0.5:0.05:5)*1e9,real(zk2),'-.g',(0.5:0.05:5)*1e9,imag(zk2),'-.k');
legend('RIteration2','XIteration2','RIteration4','XIteration4');

In the legend, 'R' represents resistance curve and 'X' represents Reactance curve.

Tabulation of resonant frequencies, electrical lengths of dipole, fractal koch with second and fourth iteration.

Iteration = [0;2;4]; % Zeroth iteration corresponds to dipole antenna.
ResonantFrequencies_GHz = {'2.35';'0.87,1.54, 2.5, 3.04, 4.04, 4.53';'0.7, 1.25, 2.05, 2.5, 3.25,3.7,4.5'};
PhysicalLength = [60e-3;60e-3;60e-3];
ElectricalLength = [60e-3; 106.7e-3; 189.6e-3];
table(Iteration,ResonantFrequencies_GHz,PhysicalLength,ElectricalLength)

ans =

  3x4 table

    Iteration           ResonantFrequencies_GHz            PhysicalLength    ElectricalLength
    _________    ______________________________________    ______________    ________________

        0        {'2.35'                              }         0.06                0.06     
        2        {'0.87,1.54, 2.5, 3.04, 4.04, 4.53'  }         0.06              0.1067     
        4        {'0.7, 1.25, 2.05, 2.5, 3.25,3.7,4.5'}         0.06              0.1896

With number of iterations equal to two, the antenna is resonating at six frequencies where the first resonating frequency is 0.87 GHz with the electrical length of koch 106.7 mm. The first resonant frequency is shifted left when compared to the resonant frequency of dipole antenna. This helps us to create a koch dipole of physical length less than the length of dipole. With number of iterations equal to four,the antenna is resonating at eight frequencies where the first resonant frequency is 0.7 GHz. There is an increase in number of resonating frequencies and there is a left shift in the resonating frequencies when number of iterations are increased. The total length of the curve is 189.6 mm ((4/3)^n*(k.Length), n = 4).

Create a koch dipole antenna of four iterations with physical length of 19 mm, which makes electrical length 60 mm((4/3)^4*19e-3 = 60e-3). And plot impedance over the frequency range of 0.5 GHz - 5 GHz.

antK = fractalKoch('Length',19e-3);
figure;impedance(antK,(1.5:0.05:5.5)*1e9);

The impedance plot shows that the koch dipole antenna is resonating at 2.75 GHz which is closer to the dipole antenna resonating frequency. But the physical length of koch dipole is 19 mm whereas the dipole length is 60 mm. So, the size of the antenna is reduced by 68 percentage. Miniaturization is one of the advantages of fractals.

Fractal Koch Loop Vs Circular Loop Antenna

Create a circular loop antenna which resonates at 1 GHz.

antL = design(loopCircular,1e9);
figure;show(antL);

Design a fractal koch loop antenna which resonates at 1 GHz. Koch loop antenna is constructed by using koch curve.

antkL = design(fractalKoch('Type','loop'),1e9);
figure;show(antkL);

The radius of circular loop antenna is 52.1 mm. The perimeter is 327.2 mm. The radius of circle which circumscribes the koch loop of side 74 mm is sqrt(3)*74e-3, which is equal to 42.8 mm. This value is less than the radius of circular loop antenna for the same resonant frequency 1GHz. The perimeter with two iterations of koch loop is 395.4 mm (3*sqrt(3)*(4/3)^n*radius). Further, the perimeter of the koch loop can be increased by increasing number of iterations. With number of iterations equal to four, the perimeter of loop is 702.9 mm which is 2.14 times longer than the perimeter of circular loop. The advantage is the perimeter increases while maintaining the same volume occupied.

Fractal Carpet Antenna

A square is taken and virtually (zeroth iteration) divided into 9 smaller congruent squares, each of which is one-third of the original square and the center square was removed to get the first iteration. Similarly, for the second iteration subdivide each of the eight remaining solid squares into 9 congruent squares and remove the center square. Continue in the same fashion to obtain further iterations of the carpet.

Create a fractal carpet antenna with a substrate of dielectric constant 4.4 and loss tangent 0.03 and with number of iterations equal to one.

antC = fractalCarpet;
antC.NumIterations = 1;
sub = dielectric('EpsilonR',4.4,'LossTangent',0.03);
antC.Length = 27.9e-3;
antC.Width = 37.25e-3;
antC.Substrate = sub;
antC.Height = 1.59e-3;
antC.GroundPlaneLength = 48e-3;
antC.GroundPlaneWidth = 57e-3;
antC.FeedOffset= [-0.5*antC.GroundPlaneLength -6e-3];

Mesh the antenna with a maximum edge length of 20e-3.

mesh(antC,'MaxEdgeLength',20e-3);

Calculate impedance, s-parameters over the frequency range of 1.5 GHz to 5 GHz.

freqRange = ((1.5:0.02:5)*1e9);
z1 = impedance(antC,freqRange);
s1 = sparameters(antC,freqRange);

Change number of iterations to two.

antC.NumIterations = 2;
figure;show(antC);

Calculate the impedance with second iteration and plot the impedance of first and second iterations.

z2 = impedance(antC,freqRange);
figure;plot(freqRange,real(z1),'b',freqRange,imag(z1),'r'); grid on;
hold on;plot(freqRange,real(z2),'-g',freqRange,imag(z2),'-k');
legend('RIteration1','XIteration1','RIteration2','XIteration2');

The fractal carpet antenna is resonating at multiple frequencies. This is due to the self-similarity in the geometry of the antenna. The resonant frequencies for fractal carpet with number of iterations two are shifted left when compared to the number of iterations equal to one.

Calculate the s-parameters in second iteration and plot for first and second iterations.

s2 = sparameters(antC,freqRange);
figure;rfplot(s1);
hold on;rfplot(s2);
legend('Iteration1','Iteration2');

Tabulation of bandwidths and magnitudes of reflection coefficient with first and second iterations.

Iteration = [1;2;2];
FrequencyRange_GHz = {'3.84-3.92';'3.18-3.24';'3.8-3.88'};
ReflectionCoefficients_dB = [-14.22; -11.95; -15.64];
Bandwidth_MHz = [80;60;80];
table(Iteration,FrequencyRange_GHz,Bandwidth_MHz,ReflectionCoefficients_dB)

ans =

  3x4 table

    Iteration    FrequencyRange_GHz    Bandwidth_MHz    ReflectionCoefficients_dB
    _________    __________________    _____________    _________________________

        1          {'3.84-3.92'}            80                   -14.22          
        2          {'3.18-3.24'}            60                   -11.95          
        2          {'3.8-3.88' }            80                   -15.64

With number of iterations one, the reflection coefficient is less than -10dB in one band. With number of iterations two, there are two bands of frequencies as mentioned in the table. The self-similarity property of fractals gives the multi band behavior. So, fractal antennas can be used in different bands of frequencies. The area of fractal carpet gets decreased by (8/9)^n times the original area of square patch, with the increase in number of iterations(n). With n = 1, there is 11.1 percentage reduction in area and with n = 2, there is 21 percent reduction in area compared to the area with zeroth iteration.

Conclusion

Applying fractal geometries is one of the ways to miniaturize antennas. With the increase in number of iterations, the electrical length of dipole, perimeter of koch loop increases. This increase helps in fitting large electrical length into smaller volume. There is a decrease in the dimensions of the fractal antennas, compared to the conventional antennas. The self-similarity in the geometry of the fractal antennas, helps them operate in multi bands. Miniaturization and multi band characteristics can be observed with the other fractals also like fractal gasket, fractal snowflake, and fractal Island antennas.

References

[1] Werner, D. H. and S. Ganguly, "An overview of fractal antenna engineering research", IEEE Antennas and Propagation Magazine, Vol. 45, No. 1, 38-57, 2003.

[2] "Design and Implementation of Sierpinski Carpet Fractal Antenna for Wireless Communication. Rahul Batra, P.L.Zade, Dipika.