Using Sensitivity Analysis to Optimize Powertrain Design for Fuel Economy
By Aditya Baru, MathWorks
If you’ve shopped for a new car recently, chances are you’ve seen stickers like this on vehicles in the showroom:
In the United States it’s called a Monroney sticker. Automobile manufacturers are required to display it on all new vehicles so that customers know what kind of mileage they can expect. Fuel economy is not only an important factor for car buyers; it is also a serious concern for environmental regulation agencies, who are proposing standards aimed at increasing gas mileage over the coming years.
Apart from this concern, several automakers have recently been sued by consumers for posting Monroney sticker fuel economy numbers that do not accurately reflect “real-world driving.” Discrepancies between real-world fuel economy numbers and Monroney sticker numbers have increased significantly over the past few years. This is because today’s control systems perform extremely well in the pre-defined scenarios used for Monroney mileage estimates. However, when the car is driven under real-world conditions, such as at faster speeds on highways, fuel consumption can differ from the sticker number. As you can imagine, there is a lot of interest among auto manufacturers in understanding what engineering decisions can be made to reduce variability in real-world fuel economy by making their control systems more robust to changes in driving conditions.
As a result, engineers are being asked to understand which parameters have the greatest impact on the behavior of their control systems and the fuel efficiency of their vehicles. In this article, we’ll describe an interactive workflow that uses Monte Carlo simulations and sensitivity analysis to determine which components in a car’s powertrain have the greatest impact on fuel economy. By identifying these components, we can take steps such as tweaking the design to reduce fuel consumption or make the control system more robust to changes in those components’ parameters to meet the required fuel economy values.
The workflow is based on the Sensitivity Analysis tool in Simulink Design Optimization™. We will be considering a passenger car with a conventional gasoline engine, and will take into account the differences in driving on the highway and in the city. While this article focuses on identifying parameters that impact fuel economy, the approach described can be used to analyze the sensitivity of any system that is subject to variations in its design parameters.
Modeling the System
To perform Monte Carlo simulations and the subsequent sensitivity analysis, we first need a model that captures the dynamics of the vehicle and describes it in terms of its various components. In our example, the model will need to be defined in terms of parameters that can influence the vehicle’s fuel consumption, such as the drive wheel radius, the axle ratio, and even environmental conditions such as the temperature. We can then shortlist the parameters of interest and generate a set of samples to use for Monte Carlo simulations.
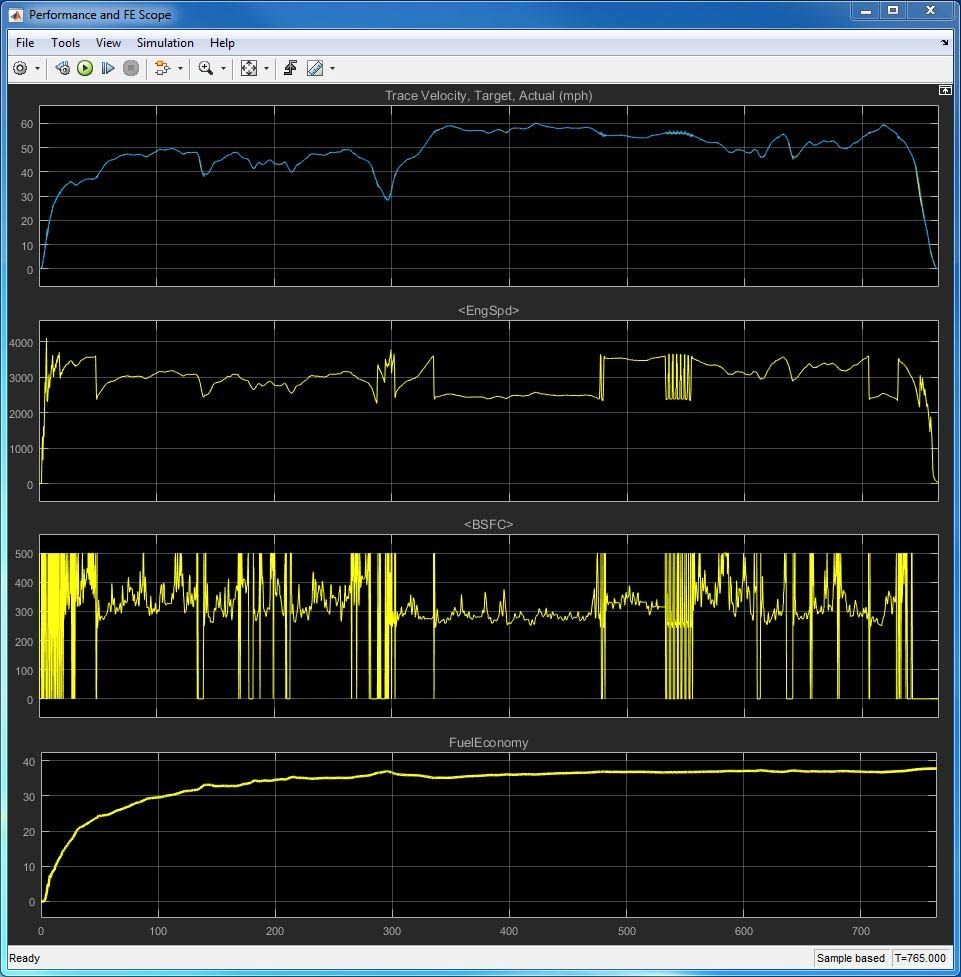
In this example we are using a Simulink® model available in Powertrain Blockset™ (Figure 1). This model of a conventional gasoline vehicle with a spark ignition engine and an 8-speed dual clutch transmission includes environmental conditions as well as vehicle components.
We’ll start by running a baseline simulation using the FTP75 drive cycle data specified by the U.S. EPA to automakers selling in the U.S. The simulation results show that for approximately 40 minutes of city driving, our gas mileage is around 30 mpg (Figure 2).
Setting Up Monte Carlo Simulations
For the Monte Carlo simulations, we will be determining the impact of five parameters on gas mileage:
- Vehicle mass
- Wheel radius
- External barometric pressure
- Throttle bore diameter
- Injector slope
The vehicle mass and the wheel radius are self-explanatory. The external barometric pressure refers to the atmospheric pressure of the surrounding environment. The throttle bore diameter influences airflow into the engine, while the injector slope affects the fuel flow through the fuel injectors, which determines the engine power. Throttle bore and injector slope variations can be caused by component manufacturing variation and by part aging, such as “throttle coking” and fuel deposits on injector pintles. We have chosen a smaller set of parameters here for simplicity, but the set can be expanded to include parameters such as the number of cylinders, the cylinder volume, and any other parameter defined in the model.
To create a new parameter set containing the five parameters listed above, we simply press the “Select Parameters” button in the Sensitivity Analysis tool. Next, we create a sample set that will cover a design space large enough to show how each of the five parameters affects the mileage. We could create this sample set using fixed, known values, but we’ll be using a quasi-random sequence―the Sobol sequence―to cover a large range of possible values evenly and efficiently. Other sample-generation methods include random sampling and multivariate distribution-based sampling.
We can specify the probability distribution to be used for generating samples for each parameter and set upper and lower bounds on the possible values. For example, we assume that the vehicle mass is uniformly distributed between 1200 kilograms and 1400 kilograms, corresponding to the weight of the car with one occupant and four occupants, respectively. We set similar bounds for the other four parameters and generate 100 samples, which we then plot (Figure 3).
Next, we select the signal in our model that calculates the mileage for this particular city drive cycle. In our case, the Simulink signal we select, available in the “Visualization” subsystem, provides a continuous estimate of the fuel efficiency. By looking at the final value of this signal, we get an estimate of the mpg value for that particular simulation. We then click the “Evaluate Model” button in the Sensitivity Analysis tool to evaluate the entire set of parameters. The tool runs a simulation of the model for each row of samples and calculates the value of interest (in our case, the mpg) for each simulation. In this particular model, the mpg value is estimated by a signal in the “Visualization” subsystem. We can then perform a sensitivity analysis for the mpg value based on these results.
The Sensitivity Analysis tool can run parallel simulations, which is especially important when we consider the large numbers of drive-cycle runs required for sensitivity analysis. The given set of parameters is evaluated automatically in parallel by workers in the cluster we have connected to, and the results are visualized in a scatter plot (Figure 4). The x-axes show the variations in the five parameter values, while the y-axis shows the value of the calculated mileage for each sample. The scatter plot shows that for this set of parameters, the vehicle’s mpg can vary between 24 and 32 for the same drive cycle.
Analyzing the Sensitivity of MPG to Parameter Variations
We can overlay a linear fit on the scatter plot to identify trends in the simulation data (Figure 5). From this fit, we can see that the mpg value for city driving improves as the wheel radius increases. Similarly, we see that the lighter the car, the better the fuel efficiency.
Alternatively, we can calculate mpg sensitivity to parameter variations using a more statistical approach with the Sensitivity Analysis tool. We can use the tool to calculate statistical values such as the correlation coefficients for the mpg value with respect to the parameter variations. In this example, we’ll be looking at the correlation values, represented using the tornado plot shown in Figure 5.
The plot shows that the mpg value correlates positively with the wheel radius and negatively with the vehicle mass. This tells us that the mpg value improves with an increase in the wheel radius and with a reduction in the vehicle mass. Based on the size of the bar in the plot, which is determined by the correlation coefficient, we also see that the influence of the wheel radius on mpg is greater than that of the vehicle mass. Similarly, the mpg value improves with a decrease in the injector slope, and changes in the values of the throttle bore and the external pressure have very little impact on fuel consumption, as evidenced by their low correlation values.
We then look at how driving on a highway can impact fuel economy. The simulation results for a 13-minute highway drive are shown in Figure 6. This simulation uses the HWFET drive cycle data specified by the EPA, and the mileage we see is around 35 mpg. We run the Monte Carlo simulations and perform a sensitivity analysis for this highway driving cycle using the same set of samples as before. As the tornado plot for the correlation coeffcients shows, barometric pressure has the greatest effect, with the mileage increasing as the external pressure falls. The effect of other parameter variations, such as the injector slope or the vehicle mass, is much smaller (Figure 7).
As we can see, the impact of the various parameters is dramatically different for the two drive cycles we’ve used. This difference can be attributed to the fact that the engine is running under different operating conditions for the drive cycles used. This can be seen by comparing the engine speed (second axis) in Figures 2 and 6. The engine speed is more “spiky” for the city drive cycle and more uniform for the highway drive cycle. At higher altitudes, where air pressure is lower, the throttle needs to be more open for a given torque output. The result is fewer energy losses, which improves fuel economy. Consequently, the impact of the barometric pressure turns out to be much higher for highway driving than it is for city driving (Figure 7).
It must be noted that these results are heavily dependent on the samples in the dataset. If we were to run the Monte Carlo simulations for a narrower range of wheel radius values or for a much wider range of vehicle mass values, we would expect to see different results for the sensitivity analysis.
Improving Monte Carlo Simulation Performance Using Parallel Computing
Our Simulink model has more than 6000 blocks and contains model references, variants, and data dictionaries that allow different teams to use it for multiple applications. The size of the model makes running hundreds or thousands of simulations on a local desktop very time-consuming. To improve performance, we run the simulations in parallel. There are several ways to do this. We could use the desktop’s parallel computing capabilities using Parallel Computing Toolbox™, or access a high-performance cluster on the network that is running MATLAB®. In this case, we use a 12-core cluster running MATLAB Parallel Server™ that is available on a local network, to reduce the total simulation time by a factor of 10.
To do this, we simply enable the use of our cluster in the Sensitivity Analysis tool Options menu. The tool then automatically finds and adds the required file and path dependencies. This ensures that each parallel worker has all the information it needs to complete a simulation successfully.
Summary and Next Steps
Our analysis showed that wheel radius has the greatest impact on city driving, while an environmental condition like barometric pressure influences highway mileage the most.
This kind of insight is what makes sensitivity analysis a useful tool: it enables engineers to better understand which tradeoffs they need to consider and how design changes will affect system behavior. In this case, engineers can ensure mpg sticker accuracy by adding special features to the controller to make fuel economy more robust to wheel diameter changes. For example, we could use wheel diameter estimation via the wheel speed sensors to adjust the transmission shift schedule to account for the diameter change and keep the engine operating within its most efficient range. Similarly, we could reduce fuel consumption for city driving by increasing the throttle bore.
Published 2017 - 93101v00