EM Algorithm for Gaussian Mixture Model (EM GMM)
This package fits Gaussian mixture model (GMM) by expectation maximization (EM) algorithm.It works on data set of arbitrary dimensions.
Several techniques are applied to improve numerical stability, such as computing probability in logarithm domain to avoid float number underflow which often occurs when computing probability of high dimensional data.
The code is also carefully tuned to be efficient by utilizing vertorization and matrix factorization.
This algorithm is widely used. The detail can be found in the great textbook "Pattern Recognition and Machine Learning" or the wiki page
http://en.wikipedia.org/wiki/Expectation-maximization_algorithm
This function is robust and efficient yet the code structure is organized so that it is easy to read. Please try following code for a demo:
close all; clear;
d = 2;
k = 3;
n = 500;
[X,label] = mixGaussRnd(d,k,n);
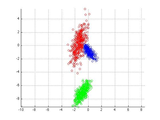
plotClass(X,label);
m = floor(n/2);
X1 = X(:,1:m);
X2 = X(:,(m+1):end);
% train
[z1,model,llh] = mixGaussEm(X1,k);
figure;
plot(llh);
figure;
plotClass(X1,z1);
% predict
z2 = mixGaussPred(X2,model);
figure;
plotClass(X2,z2);
Besides using EM to fit GMM, I highly recommend you to try another submission of mine: Variational Bayesian Inference for Gaussian Mixture Model
(http://www.mathworks.com/matlabcentral/fileexchange/35362-variational-bayesian-inference-for-gaussian-mixture-model) which performs Bayesian inference on GMM. It has the advantage that the number of mixture components can be automatically identified by the algorithm.
Upon request, I also provide a prediction function for out-of-sample inference.
This function is now a part of the PRML toolbox (http://www.mathworks.com/matlabcentral/fileexchange/55826-pattern-recognition-and-machine-learning-toolbox)
For anyone who wonders how to finish his homework, DONT send email to me.
Cite As
Mo Chen (2024). EM Algorithm for Gaussian Mixture Model (EM GMM) (https://www.mathworks.com/matlabcentral/fileexchange/26184-em-algorithm-for-gaussian-mixture-model-em-gmm), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- Signal Processing > Signal Processing Toolbox > Transforms, Correlation, and Modeling > Transforms > Discrete Fourier and Cosine Transforms > Fast Fourier Transforms >
Tags
Acknowledgements
Inspired by: Variational Bayesian Inference for Gaussian Mixture Model, Pattern Recognition and Machine Learning Toolbox
Inspired: GMMVb_SB(X), Gaussian mixture model parameter estimation with prior hyper parameters, Dirichlet Process Gaussian Mixture Model, Variational Bayesian Inference for Gaussian Mixture Model, EM algorithm for Gaussian mixture model with background noise
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
EmGm
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.16.0.1 | improve description |
||
| 1.16.0.0 | Update description
|
||
| 1.15.0.0 | tuning |
||
| 1.13.0.0 | Fix several minor bugs and reorganize the code structure a bit. |
||
| 1.12.0.0 | update loggausspdf due to api change of matlab |
||
| 1.11.0.0 | reorganize and clean the code a bit |
||
| 1.10.0.0 | fix bug for 1d data |
||
| 1.8.0.0 | fix bug for 1d data |
||
| 1.7.0.0 | Fixed missing file |
||
| 1.3.0.0 | update description |
||
| 1.2.0.0 | add missing files |
||
| 1.1.0.0 | fix missing files |
||
| 1.0.0.0 |