Coaxial Transmission Line
Model coaxial transmission line
Libraries:
RF Blockset /
Equivalent Baseband /
Transmission Lines
Description
The Coaxial Transmission Line block uses S-parameters to model its frequency behavior. A cross-section of the Coaxial Transmission Line is shown in the following figure. Its physical characteristics include the radius of the inner conductor a and the radius of the outer conductor b.

Parameters
Main
Outer radius (m) — Radius of outer conductor
2.57e-3 (default) | scalar
Radius of the outer conductor of the coaxial transmission line, specified as a scalar in meters.
Inner radius(m) — Radius of Inner conductor
0.725e-3 (default) | scalar
Radius of the inner conductor of the coaxial transmission line, specified as a scalar in meters.
Relative permeability constant — Relative permeability of dielectric
1 (default) | real scalar
Relative permeability of the dielectric, expressed as the ratio of the permeability of the dielectric to permeability in free space μ0, specified as a real scalar.
Relative permittivity constant — Relative permittivity of dielectric
2.3 (default) | real scalar
Relative permittivity of the dielectric, expressed as the ratio of the permittivity of the dielectric to permittivity in free space ε0, specified as a real scalar.
Loss tangent of dielectric — Dielectric loss tangent
0 (default) | nonnegative scalar
Loss tangent of the dielectric, specified as a nonnegative scalar.
Conductivity of the conductor (S/m) — Conductivity of conductor
inf (default) | positive scalar
Conductivity of the conductor, specified as a positive scalar in Siemens/meters.
Transmission line length (m) — Physical length of transmission line
0.01 (default) | positive scalar
Physical length of the transmission line, specified as a positive scalar in meters.
Stub mode — Type of stub
Not a stub (default) | Shunt | Series
The block enables you to model the transmission line as a stub or as a stubless line.
Stubless Transmission Line
Not a stub—Not a stubIf you model a coaxial transmission line as stubless line, the Coaxial Transmission Line block first calculates the ABCD-parameters at each frequency contained in the modeling frequencies vector. It then uses the
abcd2sfunction to convert the ABCD-parameters to S-parameters. For more information, see Stub Mode - Not a Stub.
Shunt Transmission Line
Shunt—This parameter provides a two-port network that consists of a stub transmission line that you can terminate with either a short circuit or an open circuit as shown in these diagrams.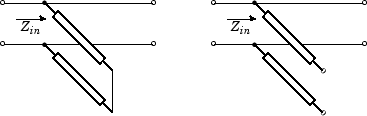
Zin is the input impedance of the shunt circuit and it is calculated as follows:
for a short circuited transmission line
and for the open circuited transmission line
where
Z0 is the characteristic impedance and
is the propagation constant
The ABCD-parameters for the shunt stub are calculated as
Series Transmission Line
Series—This mode parameter provides a two-port network that consists of a series transmission line that you can terminate with either a short circuit or an open circuit as show in these diagrams.
Zin is the input impedance of the series circuit. The ABCD-parameters for the series stub are calculated as
Termination of stub — Stub termination
Open (default) | Short
Stub termination for stub modes Shunt and
Series. Choices are Open or
Short
Dependencies
To enable this parameter, select Shunt
or Series in Stub
mode
Visualization
Source of frequency data — Frequency data source
User-specified (default)
Frequency data source, specified as
User-specified.
Frequency data (Hz) — Frequency data range
[1e9:1e6:3e9] (default) | vector
Frequency data range, specified as a vector in hertz.
Reference impedance (ohms) — Reference impedance
50 (default) | nonnegative scalar
Reference impedance, specified as a nonnegative scalar in ohms.
Plot type — Type of data plot
X-Y plane (default) | Composite data | Polar plane | Z Smith chart | Y Smith chart | ZY Smith chart
Type of data plot to visualize using the given data, specified as one of the following:
X-Y plane— Generate a Cartesian plot of the data versus frequency. To create linear, semilog, or log-log plots, set the Y-axis scale and X-axis scale accordingly.Composite data— Plot the composite data. For more information, see Create Plots Using Equivalent Baseband Library Blocks.Polar plane— Generate a polar plot of the data. The block plots only the range of data corresponding to the specified frequencies.Z smith chart,Y smith chart, andZY smith chart— Generate a Smith® chart. The block plots only the range of data corresponding to the specified frequencies.
Y parameter1 — Type of parameters to plot
S11 (default) | S12 | S21 | S22 | GroupDelay | OIP3 | IIP3 | NF | ...
Type of parameters to plot, specified as one of the following.
S11 | S12 | S21 | S22 |
GroupDelay | GammaIn | GammaOut | VSWRIn |
VSWROut | OIP3 | IIP3 | NF |
NFactor | NTemp | TF1 | TF2 |
TF3 | Gt | Ga | Gp |
Gmag | Gmsg | GammaMS | GammaML |
K | Delta | Mu | MuPrime |
Note
Y parameter1 is disabled when you select Plot type to Composite data.
Y parameter2 — Type of parameters to plot
S11 (default) | S12 | S21 | S22 | GroupDelay | OIP3 | IIP3 | NF | ...
Type of parameters to plot, specified as one of the following.
S11 | S12 | S21 | S22 |
GroupDelay | GammaIn | GammaOut | VSWRIn |
VSWROut | OIP3 | IIP3 | NF |
NFactor | NTemp | TF1 | TF2 |
TF3 | Gt | Ga | Gp |
Gmag | Gmsg | GammaMS | GammaML |
K | Delta | Mu | MuPrime |
Note
Y parameter2 is disabled when you select Plot type to Composite data.
Y format1 — Plot format
Magnitude (decibels) (default) | Mag | Magnitude (linear) | Angle | Real | Imaginary | ...
Plot format, specified as one of the following.
| Y parameter1 | Y format1 |
|---|---|
S11, S12, S21, S22, GammaIn, GammaOut, TF1, TF2, TF3, GammaMS, GammaML, and Delta. | dB, Magnitude (decibels), Abs, Mag, Magnitude (linear), Angle, Angle(degrees), Angle(radians), Real, Imag, and Imaginary. |
GroupDelay | ns, us, ms, s, and ps. |
VSWRIn and VSWROut. | Magnitude (decibels) and None. |
OIP3 and IIP3. | dBm, W, and mW. |
NF | dB and Magnitude (decibels). |
NFactor, K, Mu, and MuPrime. | None |
NTemp | Kelvin |
Gt, Ga, Gp, Gmag, and Gmsg. | dB, Magnitude (decibels), and None. |
Dependencies
To enable Y format1, set Plot type to X-Y plane.
Y format2 — Plot format
Magnitude (decibels) (default) | Mag | Magnitude (linear) | Angle | Real | Imaginary | ...
Plot format, specified as one of the following.
| Y parameter2 | Y format2 |
|---|---|
S11, S12, S21, S22, GammaIn, GammaOut, TF1, TF2, TF3, GammaMS, GammaML, and Delta. | dB, Magnitude (decibels), Abs, Mag, Magnitude (linear), Angle, Angle(degrees), Angle(radians), Real, Imag, and Imaginary. |
GroupDelay | ns, us, ms, s, and ps. |
VSWRIn and VSWROut. | Magnitude (decibels) and None. |
OIP3 and IIP3. | dBm, W, and mW. |
NF | dB and Magnitude (decibels). |
NFactor, K, Mu, and MuPrime. | None |
NTemp | Kelvin |
Gt, Ga, Gp, Gmag, and Gmsg. | dB, Magnitude (decibels), and None. |
Dependencies
To enable Y format2, set Plot type to X-Y plane.
X parameter — Frequency plot
Freq (default)
Frequency plot, specified as Freq.
X format — Frequency plot format
Hz (default) | Auto | kHz | MHz | GHz | THz
Frequency plot format, specified as one of the following.
Auto | Hz | kHz | MHz |
GHz | THz |
Y scale — Y-axis scale
Linear (default) | Log
Y-axis scale, specified as Linear or Log.
Dependencies
To enable this parameter, set Plot type to X-Y
plane.
X scale — X-axis scale
Linear (default) | Log
X-axis scale, specified as Linear or Log.
Dependencies
To enable this parameter, set Plot type to X-Y
plane.
Plot — Plot specified data
button
Plot the specified data using the plot button.
More About
Stub Mode - Not a Stub
This block calculates the ABCD-parameters using the physical length of the transmission line, d, and the complex propagation constant k using the equations:
Z0 and k are vectors whose elements correspond to the elements of f, a vector of modeling frequencies, determined by the Output Port block. Both can be expressed in terms of the resistance (R), inductance (L), conductance (G), and capacitance (C) per unit length (meters)
where
In these equations:
a is the radius of the inner conductor.
b is the radius of the outer conductor.
σcond is the conductivity of the conductor.
μ is the permeability of the dielectric. μ = μ0 μr, where:
μ0 is the permeability in free space.
μr is the Relative permeability constant
The is a complex dielectric constant given by ε = ε′ − јε″= ε′ (1 − јtanδ)
ε′ is the real part of complex dielectric constant ε, ε′ = ε0εr.
ε″ is the imaginary part of complex dielectric constant ε, ε″ = ε0εrtan δ where :
ε0 is the permittivity of free space.
εr is the Relative permittivity constant parameter value.
tan δ is the Loss tangent of dielectric parameter value.
δcond is the skin depth of the conductor, which the block calculates as .
References
[1] Pozar, David M. Microwave Engineering. Hobken, NJ, John Wiley & Sons, Inc., 2005.
Version History
Introduced in R2009a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)