flattopwin
Flat top weighted window
Description
Examples
Input Arguments
Output Arguments
Algorithms
Flat top windows are summations of cosines. The coefficients of a flat top window are computed from the following equation:
where . The coefficient values are:
| Coefficient | Value |
|---|---|
| a0 | 0.21557895 |
| a1 | 0.41663158 |
| a2 | 0.277263158 |
| a3 | 0.083578947 |
| a4 | 0.006947368 |
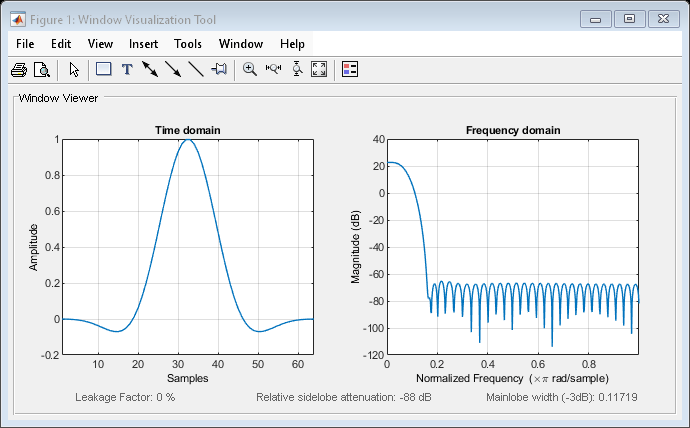
Flat top windows have very low passband ripple (< 0.01 dB) and are used primarily for calibration purposes. Their bandwidth is approximately 2.5 times wider than a Hann window.
References
[1] D’Antona, Gabriele, and A. Ferrero. Digital Signal Processing for Measurement Systems. New York: Springer Media, 2006, pp. 70–72.
[2] Gade, Svend, and Henrik Herlufsen. “Use of Weighting Functions in DFT/FFT Analysis (Part I).” Windows to FFT Analysis (Part I): Brüel & Kjær Technical Review. Vol. x, Number 3, 1987, pp. 1–28.