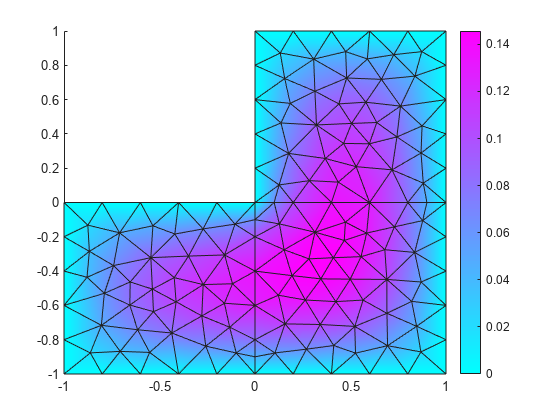
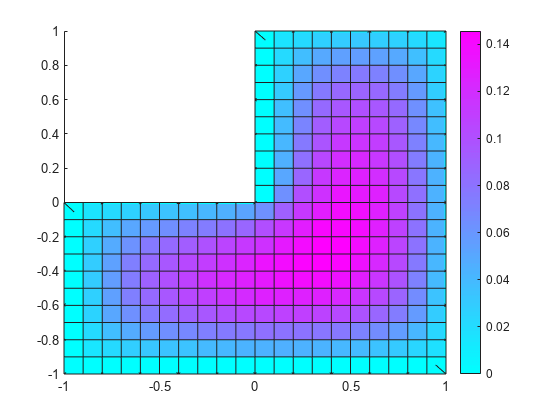
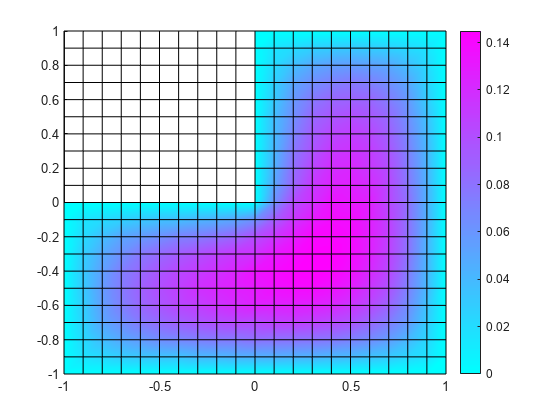
tri2grid
(Not recommended) Interpolate from PDE triangular mesh to rectangular grid
tri2grid is not recommended. Use interpolateSolution instead. For more information, see Compatibility Considerations.
Description
uxy = tri2grid(p,t,u,tn,a2,a3)tn, a2, and a3
returned by prior tri2grid call using the previous syntax to interpolate
u to the same grid as in the prior call. This syntax is efficient for
interpolating several functions to the same grid, such as interpolating hyperbolic or
parabolic solutions at multiple times.