kron
Kronecker tensor product
Syntax
Description
K = kron( returns the Kronecker tensor product
of matrices A,B)A and B. If A
is an m-by-n matrix and B
is a p-by-q matrix, then
kron(A,B) is an
m*p-by-n*q matrix formed by taking all
possible products between the elements of A and the matrix
B.
Examples
Block Diagonal Matrix
Create a block diagonal matrix.
Create a 4-by-4 identity matrix and a 2-by-2 matrix that you want to be repeated along the diagonal.
A = eye(4); B = [1 -1;-1 1];
Use kron to find the Kronecker tensor product.
K = kron(A,B)
K = 8×8
1 -1 0 0 0 0 0 0
-1 1 0 0 0 0 0 0
0 0 1 -1 0 0 0 0
0 0 -1 1 0 0 0 0
0 0 0 0 1 -1 0 0
0 0 0 0 -1 1 0 0
0 0 0 0 0 0 1 -1
0 0 0 0 0 0 -1 1
The result is an 8-by-8 block diagonal matrix.
Repeat Matrix Elements
Expand the size of a matrix by repeating elements.
Create a 2-by-2 matrix of ones and a 2-by-3 matrix whose elements you want to repeat.
A = [1 2 3; 4 5 6]; B = ones(2);
Calculate the Kronecker tensor product using kron.
K = kron(A,B)
K = 4×6
1 1 2 2 3 3
1 1 2 2 3 3
4 4 5 5 6 6
4 4 5 5 6 6
The result is a 4-by-6 block matrix.
Sparse Laplacian Operator Matrix
This example visualizes a sparse Laplacian operator matrix.
The matrix representation of the discrete Laplacian operator on a two-dimensional, n-by- n grid is a n*n-by- n*n sparse matrix. There are at most five nonzero elements in each row or column. You can generate the matrix as the Kronecker product of one-dimensional difference operators. In this example n = 5.
n = 5; I = speye(n,n); E = sparse(2:n,1:n-1,1,n,n); D = E+E'-2*I; A = kron(D,I)+kron(I,D);
Visualize the sparsity pattern with spy.
spy(A,'k')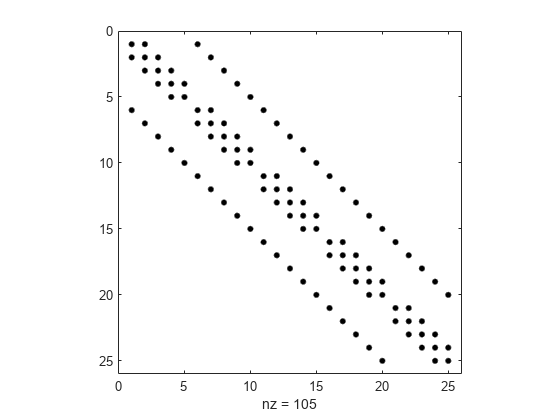
Input Arguments
A,B — Input matrices
scalars | vectors | matrices
Input matrices, specified as scalars, vectors, or matrices.
If either A or B is sparse,
then kron multiplies only nonzero elements and
the result is also sparse.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | logical
Complex Number Support: Yes
More About
Kronecker Tensor Product
If A is an m-by-n matrix
and B is a p-by-q matrix,
then the Kronecker tensor product of A and B is
a large matrix formed by multiplying B by each
element of A
For example, two simple 2-by-2 matrices produce
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
Usage notes and limitations:
Code generation does not support sparse matrix inputs for this function.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
See Also
tensorprod | hankel | toeplitz | dot | cross
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)