beta
Beta function
Syntax
Description
B = beta(Z,W)Z and W. Both
Z and W must be real and nonnegative.
Examples
Compute Beta Function for Integer Arguments
Compute the beta function for integer arguments and . Based on the definition, the beta function can be calculated as
.
Set the output format to rational to show the results as ratios of integers.
format rat
B = beta((1:10)',3)B =
1/3
1/12
1/30
1/60
1/105
1/168
1/252
1/360
1/495
1/660
Plot Beta Function
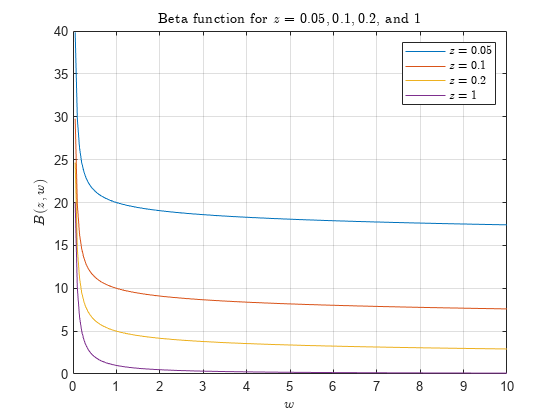
Calculate the beta function for = 0.05, 0.1, 0.2, and 1 within the interval . Loop over values of , evaluate the function at each one, and assign each result to a row of B.
Z = [0.05 0.1 0.2 1]; W = 0:0.05:10; B = zeros(4,201); for i = 1:4 B(i,:) = beta(Z(i),W); end
Plot all of the beta functions in the same figure.
plot(W,B) grid on legend('$z = 0.05$','$z = 0.1$','$z = 0.2$','$z = 1$','interpreter','latex') title('Beta function for $z = 0.05, 0.1, 0.2$, and $1$','interpreter','latex') xlabel('$w$','interpreter','latex') ylabel('$B(z,w)$','interpreter','latex')
Input Arguments
Z — Input array
scalar | vector | matrix | multidimensional array
Input array, specified as a scalar, vector, matrix, or multidimensional array. The
elements of Z must be real and nonnegative. Z and
W must be the same size, or else one of them must be a
scalar.
Data Types: single | double
W — Input array
scalar | vector | matrix | multidimensional array
Input array, specified as a scalar, vector, matrix, or multidimensional array. The
elements of W must be real and nonnegative. Z and
W must be the same size, or else one of them must be a scalar.
If
ZorWis equal to 0, the beta function returnsInf.If
ZandWare both 0, the beta function returnsNaN.
Data Types: single | double
More About
Beta Function
The beta function is defined by
The term is the gamma function
References
[1] Olver, F. W. J., A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller, and B. V. Saunders, eds., Chapter 5.12 Beta Function, NIST Digital Library of Mathematical Functions, Release 1.0.22, Mar. 15, 2018.
Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
This function fully supports tall arrays. For more information, see Tall Arrays.
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Thread-Based Environment
Run code in the background using MATLAB® backgroundPool or accelerate code with Parallel Computing Toolbox™ ThreadPool.
This function fully supports thread-based environments. For more information, see Run MATLAB Functions in Thread-Based Environment.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Distributed Arrays
Partition large arrays across the combined memory of your cluster using Parallel Computing Toolbox™.
This function fully supports distributed arrays. For more information, see Run MATLAB Functions with Distributed Arrays (Parallel Computing Toolbox).
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)