Mamdani and Sugeno Fuzzy Inference Systems
Fuzzy Logic Toolbox™ software supports two types of fuzzy inference systems:
Mamdani systems
Sugeno systems
| Fuzzy Inference System | Advantages |
|---|---|
| Mamdani |
|
| Sugeno |
|
For both Mamdani and Sugeno systems, you can create both type-1 and type-2 fuzzy systems. This topic discusses the inference processes for type-1 systems. For more information on inference for type-2 systems, see Type-2 Fuzzy Inference Systems.
Mamdani Fuzzy Inference Systems
Mamdani fuzzy inference was first introduced as a method to create a control system by synthesizing a set of linguistic control rules obtained from experienced human operators [1]. In a Mamdani system, the output of each rule is a fuzzy set.
Since Mamdani systems have more intuitive and easier to understand rule bases, they are well-suited to expert system applications where the rules are created from human expert knowledge, such as medical diagnostics.
The inference process of a Mamdani system is described in Fuzzy Inference Process and summarized in the following figure.
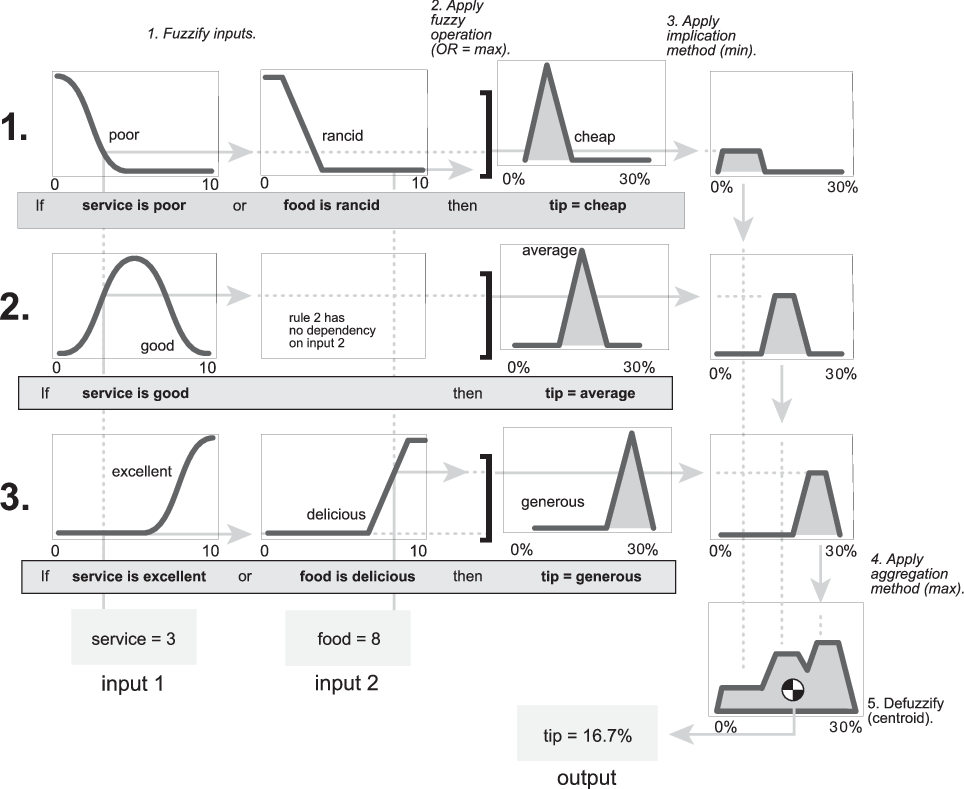
The output of each rule is a fuzzy set derived from the output membership function and the implication method of the FIS. These output fuzzy sets are combined into a single fuzzy set using the aggregation method of the FIS. Then, to compute a final crisp output value, the combined output fuzzy set is defuzzified using one of the methods described in Defuzzification Methods.
Sugeno Fuzzy Inference Systems
Sugeno fuzzy inference, also referred to as Takagi-Sugeno-Kang fuzzy inference, uses singleton output membership functions that are either constant or a linear function of the input values. The defuzzification process for a Sugeno system is more computationally efficient compared to that of a Mamdani system, since it uses a weighted average or weighted sum of a few data points rather than compute a centroid of a two-dimensional area. [2]
Each rule in a Sugeno system operates as shown in the following diagram, which shows a two-input system with input values x and y.
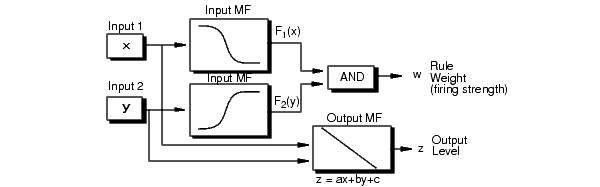
Each rule generates two values:
zi — Rule output level, which is either a constant value or a linear function of the input values:
Here, x and y are the values of input 1 and input 2, respectively, and ai, bi, and ci are constant coefficients. For a zero-order Sugeno system, zi is a constant (a = b = 0).
wi — Rule firing strength derived from the rule antecedent
Here, F1(...) and F2(...) are the membership functions for inputs 1 and 2, respectively.
The output of each rule is the weighted output level, which is the product of wi and zi.
The easiest way to visualize first-order Sugeno systems (a and b are nonzero) is to think of each rule as defining the location of a moving singleton. That is, the singleton output spikes can move around in a linear fashion within the output space, depending on the input values. The rule firing strength then defines the size of the singleton spike.
The final output of the system is the weighted average over all rule outputs:
where N is the number of rules.
The following figure shows the fuzzy inference process for a Sugeno system.
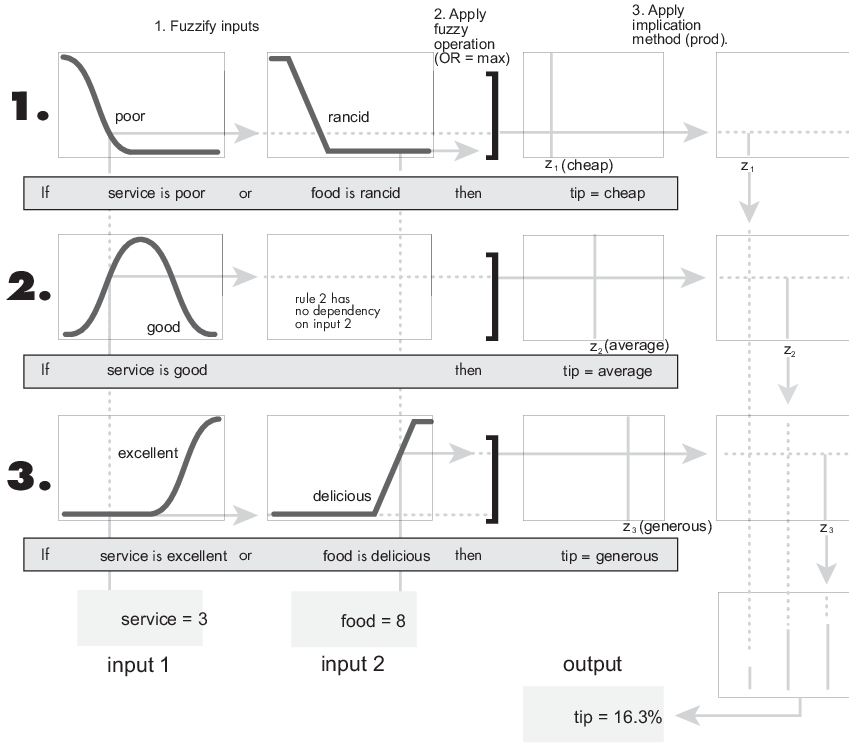
Note
Sugeno systems always use product implication and sum aggregation.
Because of the linear dependence of each rule on the input variables, the Sugeno method is ideal for acting as an interpolating supervisor of multiple linear controllers that are to be applied, respectively, to different operating conditions of a dynamic nonlinear system. For example, the performance of an aircraft may change dramatically with altitude and Mach number. Linear controllers, though easy to compute and suited to any given flight condition, must be updated regularly and smoothly to keep up with the changing state of the flight vehicle. A Sugeno fuzzy inference system is suited to the task of smoothly interpolating the linear gains that would be applied across the input space; it is a natural and efficient gain scheduler. Similarly, a Sugeno system is suited for modeling nonlinear systems by interpolating between multiple linear models.
Convert Between FIS Types
You can convert between Mamdani and Sugeno fuzzy systems.
Mamdani to Sugeno
When you convert a Mamdani system to a Sugeno system, the resulting Sugeno system has constant output membership functions that correspond to the centroids of the Mamdani output membership functions. As a result, you lose the information contained in the output membership function fuzzy sets of the Mamdani system.
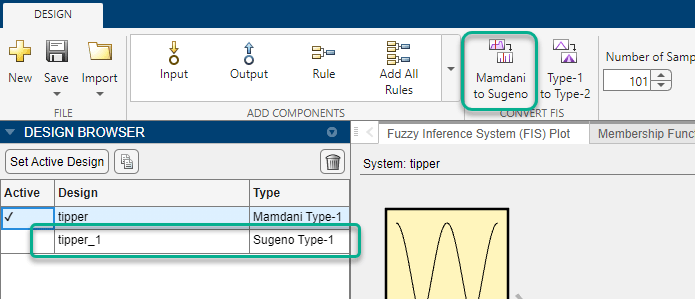
To convert a Mamdani system in the Fuzzy Logic Designer app, on the Design tab, click Mamdani to Sugeno. The app creates a Sugeno version of the active Mamdani system and adds it to the Design Browser. (since R2022b)
You can also convert a Mamdani system into a Sugeno system at the MATLAB® command line using the convertToSugeno
function. The resulting Sugeno system has constant output membership functions that
correspond to the centroids of the Mamdani output membership functions.
Sugeno to Mamdani
When you convert a Sugeno system to a Mamdani system, the resulting Mamdani system has triangular output membership functions centered at output values that match the constant term of the Sugeno output membership functions. The width of the triangular membership functions depends on the linear terms of the Sugeno membership functions.
To convert a Sugeno system in the Fuzzy Logic Designer app, on the Design tab, click Sugeno to Mamdani. The app creates a Mamdani version of the active Sugeno system and adds it to the Design Browser. (since R2022b)
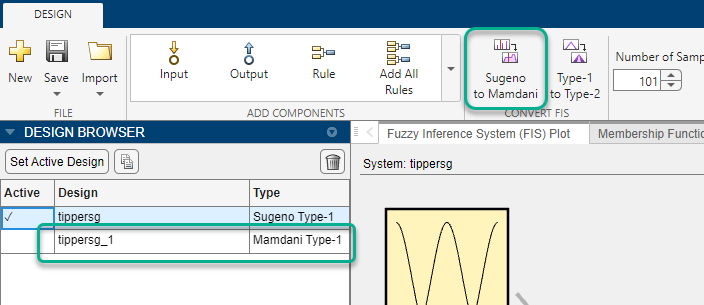
Converting a Sugeno system to a Mamdani system is not supported at the MATLAB command line.
References
[1] Mamdani, E.H., and S. Assilian. "An Experiment in Linguistic Synthesis with a Fuzzy Logic Controller". International Journal of Man-Machine Studies 7, no. 1 (January 1975): 1–13. https://doi.org/10.1016/S0020-7373(75)80002-2.
[2] Sugeno, Michio, ed. Industrial Applications of Fuzzy Control. Amsterdam ; New York : New York, N.Y., U.S.A: North-Holland; Sole distributors for the U.S.A. and Canada, Elsevier Science Pub. Co, 1985.
